cho tam giác ABC cân tại A.Vẽ đường trung tuyến AM.a,chứng minh rằng AM là đường phân giác của tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABM và ΔAMC có
AM chung
AB=AC
BM=CM
=>ΔABM=ΔACM
b: ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
c: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
MB=MC=BC/2=16cm
AM=căn 20^2-16^2=12cm
AG=2/3*AM=8cm

a: 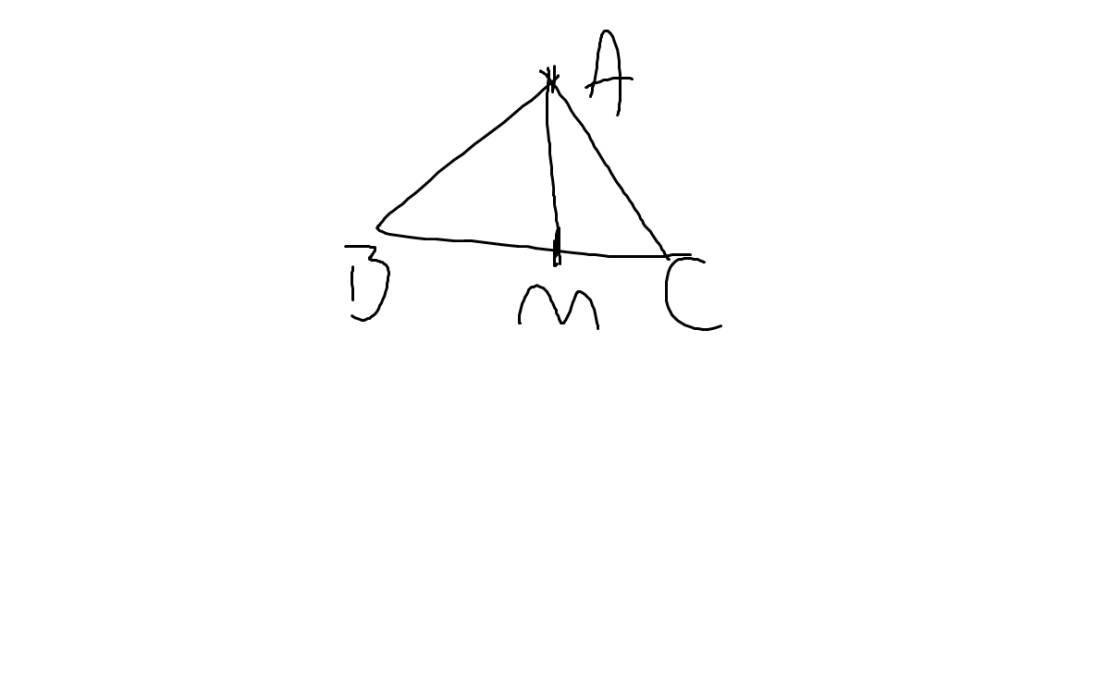
b: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC

a: M là trung điểm của BC
=>AM là đường trung tuyến của ΔABC
b: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
c: Sửa đề; tam giác ABC
AB=AC
BM=CM
=>AM là trung trực của BC

a.Ta có: AM là đường trung tuyến trong tam giác cân ABC
=> Cũng là đường cao
=> AM vuông góc với BC
b.Có AM là đường trung tuyến \(\Rightarrow BM=BC:2=32:2=16cm\)
Áp dụng định lý pytago vào tam giác vuông ABM, có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AM^2=34^2-16^2\)
\(AM=\sqrt{900}=30cm\)

Tham khảo:

Xét tam giác ABM và tam giác ACM có :
AM chung
BM = CM ( M là trung điểm BC )
AB = AC (tam giác ABC cân tại A theo giả thiết)
\( \Rightarrow \Delta AMB = \Delta AMC (c-c-c)\)
\( \Rightarrow \widehat{BAM}= \widehat{CAM}\) (2 góc tương ứng)
\( \Rightarrow \) AM thuộc tia phân giác của góc A
Mà AM cắt tia phân giác góc B tại I
\( \Rightarrow \) I là giao của các đường phân giác trong tam giác ABC
\( \Rightarrow \) CI là phân giác góc C (định lí 3 đường phân giác cắt nhau tại 1 điểm)
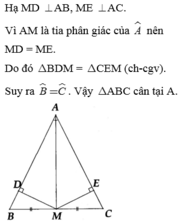
#\(N\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB = AC, `\(\widehat{B}=\widehat{C}\)
`AM` là đường trung tuyến Tam giác `ABC -> BM = MC`
Xét Tam giác `ABM` và Tam giác `ACM` có:
`AB = AC`
\(\widehat{B}=\widehat{C}\)
`BM = MC`
`->` Tam giác `ABM =` Tam giác `ACM (c-g-c)`
`->`\(\widehat{BAM}=\widehat{CAM}\) `(2` góc tương ứng `)`
`-> AM` là phân giác của \(\widehat{BAC}\)
Xét tam giác \(\Delta ABM\) và \(\Delta ACM\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABM}=\widehat{ACM}\left(gt\right)\)
\(AM\) chung
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.g.c\right)\)
Từ tam giác bằng nhau trên suy ra:
\(\widehat{BAM}=\widehat{CAM}\) nên \(AM\) là phân giác \(\widehat{BAC}\)
Là phân giác của \(\Delta ABC\)