Câu 1: Cho tam giác ABC cân tại A. Kẻ qua B tia Bx vuông góc với AB, kẻ qua C tia Cy vuông góc với AC. Gọi I là giao điểm của Bx và Cy. CMR:a, Tam giác ABI = tam giác ACIb, AI là trung trực của BCCâu 2: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N, sao cho BM=CNa, CM tam giác AMN cânb, Kẻ BH vuông góc với AM, CK vuông góc với AN. CMR BH = CKc, Gọi O là giao điểm...
Đọc tiếp
Câu 1: Cho tam giác ABC cân tại A. Kẻ qua B tia Bx vuông góc với AB, kẻ qua C tia Cy vuông góc với AC. Gọi I là giao điểm của Bx và Cy. CMR:
a, Tam giác ABI = tam giác ACI
b, AI là trung trực của BC
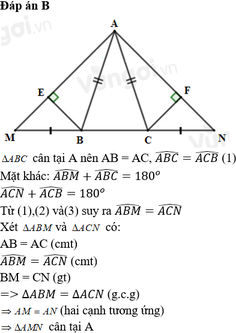
Câu 2: Cho tam giác ABC cân tại A. Trên tia đối của tia BC lấy điểm M, trên tia đối của tia CB lấy điểm N, sao cho BM=CN
a, CM tam giác AMN cân
b, Kẻ BH vuông góc với AM, CK vuông góc với AN. CMR BH = CK
c, Gọi O là giao điểm của BH và CK. CM tam giác OBC cân
d, Gọi D là trung điểm của BC. CMR 3 điểm A,D,O thẳng hàng
Câu 3: Cho tam giác ABC cân tại A, M là trung điểm của BC
a, CM tam giác ABM = tam giác ACM
b, CM AM vuông góc với BC
c, Trên cạnh AB lấy điểm E, trên cạnh CA lấy điểm F, sao cho BE = CF. CM tam giác EBC = tam giác FCB
d, CM EF//BC

a: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông góc BC
c: Xét ΔEHB vuông tại H và ΔFKC vuông tại K có
EB=FC
góc EBH=góc FCK
=>ΔEHB=ΔFKC
=>EH=FK
d: Xét ΔABH và ΔACK có
AB=AC
góc ABH=góc ACK
BH=CK
=>ΔABH=ΔACK
=>AH=AK
=>ΔAHK cân tại A
mà AM là đường cao
nên AM là phân giác của góc HAK
e: Xét ΔAHE và ΔAKF có
AH=AK
góc AHE=góc AKF
HE=KF
=>ΔAHE=ΔAKF
dài