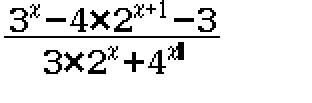giới hạn dãy số ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 1 2019
Dãy ( u n + v n ) không có giới hạn hữu hạn.
Thật vậy, giả sử ngược lại ( u n + v n ) có giới hạn hữu hạn.
Khi đó, các dãy số ( u n + v n ) v à ( u n ) cùng có giới hạn hữu hạn, nên hiệu của chúng cũng là một dãy có giới hạn hữu hạn, nghĩa là dãy số có số hạng tổng quát là u n + v n − u n = v n có giới hạn hữu hạn. Điều này trái với giả thiết ( v n ) không có giới hạn hữu hạn.
CM
2 tháng 7 2019
Vì ( u n ) có giới hạn là 0 nên | u n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi.
Mặt khác, | v n | = | | u n | | = | u n | . Do đó, | v n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi. Vậy ( v n ) có giới hạn là 0.
PT
1
CM
27 tháng 5 2018
Đáp án C
Mẹo nhanh: trên tử và mẫu của cau C ta loại trừ đi các đa thức bậc thấp hơn đi và để lại đa thức bậc cao nhất.
l i m 4 n 3 − n + 1 n n + 3 + 1 = lim 4 n 3 n n = 2.
CM
17 tháng 8 2019
Đáp án A
Ta có:
lim 2 n − 1 n = lim 2 − 1 n = 2 ≠ 0 ; lim 1 n n + 1 = 0 ; lim 1 3 n = 0 ; lim 1 n 2 + 1 = 0.
Vậy chỉ có dãy số u n = 2 n − 1 n có giới hạn khác 0.
4 tháng 4 2017
Một vài giới hạn đặc biệt của dãy số
|
Giới hạn dãy |
Giới hạn hàm |
|
lim1n=0lim1nk=0,K∈Z∗limqn=0,|q|<1limc=climnk=+∞,K∈Z∗limqn=+∞,q>1lim1n=0lim1nk=0,K∈Z∗limqn=0,|q|<1limc=climnk=+∞,K∈Z∗limqn=+∞,q>1
|
limx→x0x=x0limx→x0c=climx→±∞cxk=0,K∈z∗limx→x0x=x0limx→x0c=climx→±∞cxk=0,K∈z∗
limx→−∞xk=+∞limx→−∞xk=+∞(nếu k chẵn) limx→−∞xk=−∞limx→−∞xk=−∞(nếu k lẻ)
|
CM
23 tháng 2 2018
Đáp án C.
Dễ thấy u n = 1 1 . 3 + 1 3 . 5 + . . . + 1 2 n + 1 2 n + 3 = n 2 n + 3 ⇒ l i m u n = l i m n 2 n + 3 = 1 2 .
Lời giải:
\(\lim\limits_{x\to +\infty}\frac{3^x-4.2^{x+1}-3}{3.2^x+4^x}=\lim\limits_{x\to +\infty}\frac{(\frac{3}{4})^x-\frac{8}{2^{x}}-\frac{3}{4^x}}{3.\frac{1}{2^x}+1}=\frac{0-0-0}{0+1}=0\) (nhớ rằng $\lim q^n=0$ khi $|q|<1$)