trong một bình cách nhiệt và kín đang chứa 3l nước và một cục nước đá 500g. Người ta đổ chì lòng đang ở 327 độ c vào bình và thấy có cân bằng nhiệt ở 40 độ c. tính khối lượng chì đã đổ vào
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 11 2021
a) Nhiệt lượng thu vào để nóng chảy bình nước đá(\(0^oC\)): \(Q_1=m_1c_1\left(0-t_1\right)+m_1\lambda=1\cdot2100\cdot30+1\cdot340000=403000J\)
Nhiệt lượng nước đá tỏa ra để hạ nhiệt độ xuống \(0^oC\):
\(Q_2=m_2c_2\left(t_2-0\right)=2\cdot4200\cdot\left(48-0\right)=403200J\)
\(\Rightarrow Q_2>Q_1\),ta có nhiệt độ chung khi cân bằng nhiệt:
Nhiệt lượng 1kg nước thu vào:
\(Q'_1=m_1c_2\left(t-0\right)=4200t\left(J\right)\)
Nhiệt lượng 2kg nước tỏa ra: \(Q'_2=m_2c_2\left(t_2-t_1\right)=2\cdot4200\cdot\left(48-t\right)=403200-8400t\left(J\right)\)
Cân bằng nhiệt:
\(Q_1+Q'_1=Q'_2\Rightarrow40300+4200t=403200-8400t\)
\(\Rightarrow t=0,016^oC\)
Vậy nhiệt độ hỗn hợp khi cân bằng nhiệt là \(t=0,016^oC\)
22 tháng 12 2016
Khi được làm lạnh tới 00C, nước toả ra một nhiệt lượng bằng: Q1 = m1.C1(t – 0) = 0,5.4200.20 = 42 000JĐể làm “nóng” nước đá tới 00C cần tốn một nhiệt lượng:Q2 = m2.C2(0 – t2) = 0,5.2100.15 = 15 750JBây giờ muốn làm cho toàn bộ nước đá ở 00C tan thành nước cũng ở 00C cần một nhiệt lượng là: Q3 = λ.m2 = 3,4.105.0,5 = 170 000JNhận xét:+ Q1 > Q2 : Nước đá có thể nóng tới 00C bằng cách nhận nhiệt lượng do nước toả ra+ Q1 – Q2 < Q3 : Nước đá không thể tan hoàn toàn mà chỉ tan một phần.Vậy sau khi cân bằng nhiệt được thiết lập nước đá không tan hoàn toàn và nhiệt độ của hỗn hợp là 00C
TM
19 tháng 7 2023
gọi \(m_1\) là khối lượng bình đồng\(\left(m_1=400g=0,4kg\right)\)
\(m_2\) là khối lượng nước có trong bình ban đầu\(\left(m_2=500g=0,5kg\right)\)
\(m_3\) là khối lượng nước đá thả vào bình \(\left(m_3=320g=0,32kg\right)\)
\(m_4\) là khối lượng đá tan khi thả đá vào bình
\(m_5\) là khối lượng nước đổ thêm vào bình \(\left(m_5=1kg\right)\)
a, vì nước đá không tan hết nên nhiệt độ của hỗn hợp bằng 0 độ
ta có: \(Q_{toả}=Q_{thu}\Leftrightarrow Q_{bình}+Q_{nước}=Q_{nướcđá}+Q_{tan}\Leftrightarrow m_1.c_{Cu}.\left(40-0\right)+m_2.c_{nước}.\left(40-0\right)=m_3.c_{nướcđá}.\left[0-\left(-10\right)\right]+m_4.\lambda\Leftrightarrow0,4.400.40+0,5.4200.40=0,32.2100.10+m_4.3,4.10^5\Leftrightarrow m_4=\dfrac{523}{2125}kg\)b, sau khi đổ thêm 1kg nước thì nước đá tan hết trở thành nước, hỗn hợp bắt đầu tăng nhiệt độ. gọi \(t\) là nhiệt độ cuối cùng của hỗn hợp
ta có: \(Q_{toả}'=Q_{thu}'\Leftrightarrow Q_{nướcnóng}=Q_{bình}'+Q_{nước}'+Q_{tan}'+Q_{nướcđá}\Leftrightarrow m_5.c_{nước}.\left(50-t\right)=m_1.c_{Cu}.\left(t-0\right)+m_2.c_{nước}.\left(t-0\right)+\left(m_3-m_4\right).\lambda+m_3.c_{nước}.\left(t-0\right)\Leftrightarrow1.4200.\left(50-t\right)=0,4.400.t+0,5.4200.t+\left(0,32-\dfrac{523}{2125}\right).3,4.10^5+0,32.4200.t\Leftrightarrow t\approx23,69^oC\)
VT
30 tháng 12 2018
Đáp án: C
- Giả sử nhiệt độ của hỗn hợp sau khi cân bằng là 0 0 C
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
- Ta thấy Q t h u < Q t ỏ a chứng tỏ nước đá bị tan ra hoàn toàn.
- Gọi nhiệt độ hỗn hợp sau khi cân bằng là t 0 C (t > 0)
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C , tan hết tại 0 0 C và tăng lên đến t 0 C là:
14 tháng 8 2021
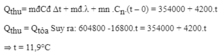
đoạn Qthu hơi nhầm lẫn xíu rối quá(bên dưới)
\(Qthu=170000M+\dfrac{1}{2}.2100.M.20+mC.20+2m.4200.20\)
\(=191000M+20mC+168000m\)
\(=>252000m+126000M=191000M+20mC+168000m\)
\(=>65000M=20m\left(4200-C\right)\left(2\right)\)
(2) chia(1)
\(=>\dfrac{260}{701}=\dfrac{2\left(4200-C\right)}{8401}=>C=...\)
14 tháng 8 2021
đá chỉ tan một nửa nên nhiệt độ cuối cùng tcb=0oC
\(=>Qthu1=\dfrac{1}{2}M.34.10^4=170000M\left(J\right)\)
\(=>Qthu2=\dfrac{1}{2}M.2100.5=5250M\left(J\right)\)
\(=>Qtoa1=m.C.10=10m\left(J\right)\)
\(=>Qtoa2=2m.4200.10=84000m\left(J\right)\)
\(=>175250M=84010m\left(1\right)\)
khi rót một lượng nước ở t3=50oC
\(=>Qtoa=\left(2m+M\right).4200.\left(50-20\right)=\left(2m+M\right)126000\left(J\right)\)
\(=252000m+126000M\left(J\right)\)
\(=>Qthu=170000M+m.C.20+2m.4200.20\)
\(=170000M+20mC+168000m\left(J\right)\)
\(=>252000m+126000M=170000M+20mC+168000m\)
\(< =>\)\(44000M=20m\left(4100-C\right)\left(2\right)\)
(2) chia(1)
\(=>\dfrac{176}{701}=\dfrac{2\left(4100-C\right)}{8401}=>C=...\)
(bài này ko chắc , bạn bấm lại máy tính nhá , dài quá sợ sai)
26 tháng 8 2016
Đổi: \(500g=0,5kg,50g=0,05kg\)
Nhiệt lượng nước thu vào để đạt đến \(55^0C\) là :
\(Q_{thu}=m_n.c_n.\Delta t=94500\left(J\right)\)
Giả sử ta đổ cùng một lúc một khối nước có khối lượng gồm n cốc vào bình.
\(\Rightarrow\) Khối lượng khối nước đó là : \(m=n.0,05\)
\(\Rightarrow\)Nhiệt lượng mà khối nước tỏa ra là: \(Q=m.c_n.\Delta t=n.0,05.4200.5=1050.n\left(J\right)\)
\(\Rightarrow1050.n=94500\)
\(\Rightarrow n=90\)
Vậy ta cần đổ - múc tối thiểu 90 lượt thì sẽ được nước có yêu cầu như đề bài!!
26 tháng 1 2018
Đâu phải nhiệt toả ra của mỗi cốc nước nước luôn bằng nhau trong mỗi lượt đâu mà bạn chia