cho đường tròn tâm O và đường tròn tâm I cắt nhau tại A và B.Tiếp tuyến tại A của đường tròn tâm O và đường tròn tâm I cắt đường tròn tâm I và O lần lượt tại D và C.a,Chứng minh AD²=BC×BD.b,Tam giác BDI là tam giâc cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét (O) có
ΔAHM nội tiếp
AH là đường kính
Do đó: ΔAHM vuông tại M
=>HM\(\perp\)AC tại M
Xét (O) có
ΔADH nội tiếp
AH là đường kính
Do đó:ΔADH vuông tại D
=>HD\(\perp\)AB tại D
Xét ΔHAB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HM là đường cao
nên \(AM\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AM\cdot AC\)
=>AD/AC=AM/AB
Xét ΔAMD và ΔABC có
AM/AB=AD/AC
góc MAD chung
Do đó: ΔAMD đồng dạng với ΔABC
=>\(\widehat{AMD}=\widehat{ABC}\)
mà \(\widehat{AMD}+\widehat{DMC}=180^0\)(hai góc kề bù)
nên \(\widehat{DMC}+\widehat{DBC}=180^0\)
=>DMCB là tứ giác nội tiếp

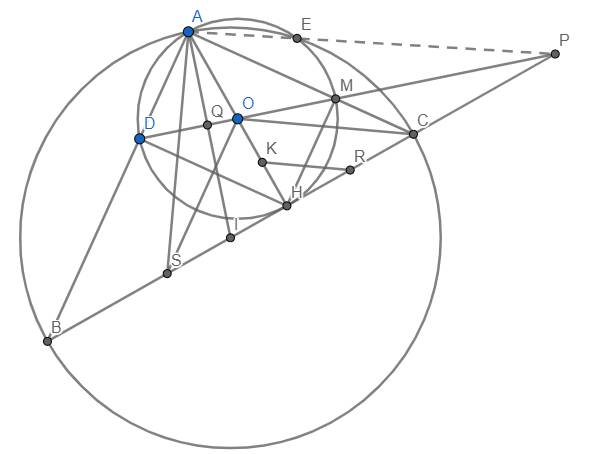
a) Chứng minh tam giác ABH vuông tại H và \(DH\perp AB\) rồi dùng hệ thức lượng \(\Rightarrow AD.AB=AH^2\). Tương tự, ta có \(AM.AC=AH^2\). Do đó \(AD.AB=AM.AC\) và theo bổ đề quen thuộc thì tứ giác BCMD nội tiếp. (đpcm)
b) Gọi Q là giao điểm của DM và AI. Khi đó tam giác ABC vuông tại A có trung tuyến AI nên \(IA=IB=IC=\dfrac{BC}{2}\) hay tam giác IBA cân tại I, suy ra \(\widehat{B}=\widehat{DAQ}\).
Lại có \(\widehat{B}+\widehat{ACB}=90^o\) suy ra \(\widehat{DAQ}+\widehat{ADQ}=90^o\) (do \(\widehat{ADQ}=\widehat{ACB}\) (cmt)). Do đó \(PQ\perp AI\) tại Q. Từ đó dễ dàng chứng minh O là trực tâm tam giác AIP.
c) Do tứ giác BCMD nội tiếp nên \(PM.PD=PC.PB\) \(\Rightarrow P_{P/\left(O\right)}=P_{P/\left(I\right)}\) \(\Rightarrow\) P nằm trên trục đẳng phương của (O) và (I). Lại có AE chính là trục đẳng phương của (O) và (I) nên A, E, P thẳng hàng. (đpcm)
d) Ta thấy SO//AB \(\perp AC\) và \(AH\perp BC\) nên O là trực tâm tam giác ASC \(\Rightarrow OC\perp AS\)
Lại có OC//KR nên \(RK\perp SA\) (đpcm)
Ở bài này chứng minh được \(A\in\left(I\right)\) vì BC là đường kính của (I) và \(\widehat{BAC}=90^o\)

a: góc BEC=góc BDC=1/2*sđ cung BC=90 độ
=>CE vuông góc AB, BD vuông góc AC
góc AEH=góc ADH=90 độ
=>AEHD nội tiếp đường tròn đường kính AH
=>I là trung điểm của AH
b: Gọi giao của AH với BC là N
=>AH vuông góc BC tại N
góc IEO=góc IEH+góc OEH
=góc IHE+góc OCE
=90 độ-góc OCE+góc OCE=90 độ
=>IE là tiếp tuyến của (O)
b: Xét ΔIBD co IB=ID
nên ΔIBD cân tại I