Cho h/s f(x) liên tục và x/đ trên [-1 ; \(+\infty\)] và t/m : \(f\left(x+1\right)+3f\left(3x+2\right)-4f\left(4x+1\right)-f\left(2^x\right)=\dfrac{3}{\sqrt{x+1}+\sqrt{x+2}}\forall x\in\left[-1;+\infty\right]\)
Tính \(\int\limits^2_1\dfrac{f\left(x\right)}{x}dx\) = ?

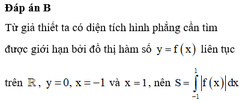

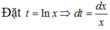
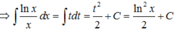
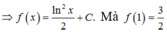
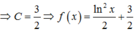
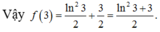
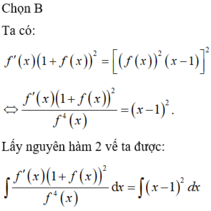
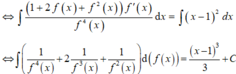
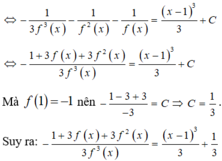
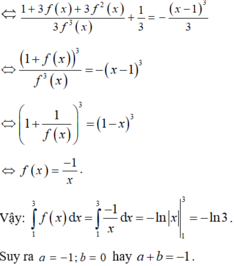
Từ GT ta lấy tích phân 2 vế cận từ 0 đến 1 ; sẽ được :
\(\int\limits^1_0f\left(x+1\right)dx+\int\limits^1_03f\left(3x+2\right)dx-\int\limits^1_04f\left(4x+1\right)dx-\int\limits^1_0f\left(2^x\right)dx=\int\limits^1_0\dfrac{3dx}{\sqrt{x+1}+\sqrt{x+2}}\left(1\right)\)
\(\int\limits^1_0\dfrac{3dx}{\sqrt{x+1}+\sqrt{x+2}}=\int\limits^1_03\left(\sqrt{x+2}-\sqrt{x+1}\right)dx\) =
\(2\left[\left(x+2\right)\sqrt{x+2}-\left(x+1\right)\sqrt{x+1}\right]\dfrac{1}{0}\) = \(2+6\sqrt{3}-8\sqrt{2}\left(2\right)\)
Dễ thấy : \(\int\limits^1_0f\left(x+1\right)dx=\int\limits^2_1f\left(t\right)dt=\int\limits^2_1f\left(x\right)dx\)
\(\int\limits^1_03f\left(3x+2\right)dx=\int\limits^5_2f\left(t\right)dt=\int\limits^5_2f\left(x\right)dx\) (3)
\(\int\limits^1_04f\left(4x+1\right)=\int\limits^5_1f\left(t\right)dt=\int\limits^5_1f\left(x\right)dx\left(4\right)\)
\(\int\limits^1_0f\left(2^x\right)dx=\int\limits^2_1\dfrac{f\left(t\right)dt}{tln2}=\dfrac{1}{ln2}.\int\limits^2_1\dfrac{f\left(t\right)dt}{t}=\dfrac{1}{ln2}.\int\limits^2_1\dfrac{f\left(x\right)dx}{x}\) (5)
Thay (2) ; (3) ; (4) ; (5) vào (1) ta được :
\(\int\limits^2_1f\left(x\right)dx+\int\limits^5_2f\left(x\right)dx-\int\limits^5_1f\left(x\right)dx-\dfrac{1}{ln2}.\int\limits^2_1\dfrac{f\left(x\right)dx}{x}=2+6\sqrt{3}-8\sqrt{2}\)
\(\Leftrightarrow\int\limits^2_1\dfrac{f\left(x\right)dx}{x}=\left(2+6\sqrt{3}-8\sqrt{2}\right)ln2\)