Bài 1: Cho \(\Delta ABC\)\(⊥\)tại A có AB=16 cm, AC=30 cm, Tính tổng các khoảng cách từ trọng tâm G của \(\Delta ABC\)đến các đỉnh của\(\Delta\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 7 2023
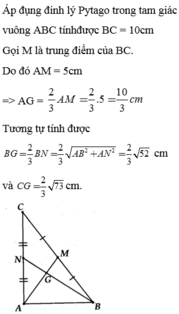
Gọi AM,BN,CE lần lượt là các đường trung tuyến của ΔABC
=>AM,BN,CE đồng quy tại G
BC=căn 6^2+8^2=10cm
=>AM=5cm
=>AG=10/3cm
AN=8/2=4cm
=>BN=căn 6^2+4^2=2*căn 13(cm)
=>BG=2/3*2căn 13=4/3*căn 13(cm)
AE=6/2=3cm
CE=căn 3^2+8^2=căn 73(cm)
=>CG=2/3*căn 73(cm)
24 tháng 4 2018
\(BC=\sqrt{AB^2+AC^2}\)
\(BC=\sqrt{16^2+30^2}\)
\(BC=34\left(cm\right)\)
Ta có: Tam giác ABC vuông tại A
\(MC=\sqrt{AC^2+AM^2}\)
\(MC=\sqrt{30^2+8^2}\)
\(MC=2\sqrt{241}\left(cm\right)\)
\(AM=\frac{1}{2}.BC=\frac{1}{2}.34=17\left(cm\right)\)
\(BD=\sqrt{AB^2+AD^2}\)
\(BD=\sqrt{16^2+15^2}=\sqrt{481}\left(cm\right)\)
Khoảng cách từ trọng tâm G của tam giác là: 2/3
20 tháng 4 2019
a, T/g AMC= t/g BMD(c-g-c)
b,T/g AMC= t/g BMD(c-g-c) \(\Rightarrow\widehat{DBM}=\widehat{ACM}\) mà chúng ở vị trí so le trong \(\Rightarrow BD\)song song AC
c, Diện tích tam giác ABC là : (3.4):2=6(cm) (1) hay (BC.AM):2(2) ;Áp dụng đlí Py-ta-go vào tam giác ABC ta được BC=5cm (3)
Từ (1);(2);(3) \(\Rightarrow\)5.AM=12 \(\Rightarrow AM=\frac{12}{5}=2,4cm\)
d, Khoảng cách từ đỉnh A đến trong tâm G là \(\frac{2}{3}\)
Hok tốt (Hình dễ tự vẽ nha)
29 tháng 4 2019
Bài 1: Áp dụng Định lý Pythagoras cho tam giác vuông ABC:AB2+AC2=BC2=>BC2=122+162=400=>BC=20(cm).
Áp dụng Định lý:"Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền"cho tam giác ABC:AM=\(\frac{1}{2}\)BC=\(\frac{1}{2}\).20=10cm
Do G là trọng tâm nên:AG=\(\frac{2}{3}\)AM=\(\frac{2}{3}\).10\(\approx\)6.7cm
Bài 2:
a) Xét \(\Delta\)ABD và \(\Delta\)ACE:
ADB=AEC=90
BAC:chung
AB=AC(\(\Delta\)ABC cân tại A)
=> \(\Delta\)ABD =\(\Delta\)ACE (Cạnh huyền-góc nhọn)
b) \(\Delta\)ABD =\(\Delta\)ACE (chứng minh trên)=>AD=AE=> \(\Delta\)AED cân tại A
c) Dễ thấy: H là trực tâm của tam giác ABC
Mà \(\Delta\)ABC cân tại A
Nên H cũng đồng thời là tam đường tròn ngoại tiếp tam giác ABC
Hay AH là đường trung trực của tam giác ABC