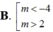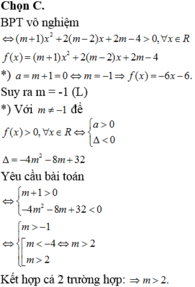tìm giá trị của m để phương trình vô nghiệm x/x-m-2m/x+m=8m^2/x^2-m^2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


f(x) = (m + 1) x 2 - 2(3 - 2m)x + m + 1 ≥ 0 (1)
Với m = -1:
(1) ⇔ -10x ≥ 0 ⇔ x ≤ 0
Vậy với m = -1 bất phương trình (1) có nghiệm x ≤ 0
Suy ra, m = -1 (loại)
Với m ≠ -1:
f(x) = (m +1 ) x 2 - 2(3 - 2m)x + m + 1
Δ' = [-(3 - 2m) ] 2 - (m + 1)(m + 1) = (2m - 3 ) 2 - (m + 1 ) 2
= (2m - 3 + m + 1)(2m - 3 - m - 1) = (3m - 2)(m - 4)
Để bất phương trình (1) vô nghiệm thì:
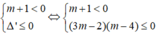
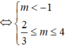
Vậy không có giá trị nào của m để bất phương trình (1) vô nghiệm

Chọn C.
Với m = 1 thỏa mãn yêu cầu bài toán
Với m ≠ 1 phương trình vô nghiệm khi và chỉ khi Δ' < 0
⇔ (m - 1 ) 2 - 2m(m - 1) < 0 ⇔ (m - 1)(-m - 1) < 0
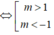
Vậy với 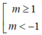 thì phương trình có nghiệm
thì phương trình có nghiệm

(m - 2)x2 + 2(2m - 3)x + 5m - 6 = 0 (1)
- Nếu m - 2 = 0 ⇔ m = 2, khi đó phương trình (1) trở thành:
2x + 4 = 0 ⇔ x = -2 hay phương trình (1) có một nghiệm
Do đó m = 2 không phải là giá trị cần tìm.
- Nếu m - 2 ≠ 0 ⇔ m ≠ 2 ta có:
Δ' = (2m - 3)2 - (m - 2)(5m - 6)
= 4m2 - 12m + 9 - 5m2 + 6m + 10m - 12
= -m2 + 4m - 3 = (-m + 3)(m - 1)
(1) vô nghiệm ⇔ Δ' < 0 ⇔ (-m + 3)(m - 1) < 0 ⇔ m ∈ (-∞; 1) ∪ (3; +∞)
Vậy với m ∈ (-∞; 1) ∪ (3; +∞) thì phương trình vô nghiệm.

\(a,x^2-\left(2m-3\right)x+m^2=0-vô-ngo\)
\(\Leftrightarrow\Delta< 0\Leftrightarrow[-\left(2m-3\right)]^2-4m^2< 0\Leftrightarrow m>\dfrac{3}{4}\)
\(b,\left(m-1\right)x^2-2mx+m-2=0\)
\(m-1=0\Leftrightarrow m=1\Rightarrow-2x-1=0\Leftrightarrow x=-0,5\left(ktm\right)\)
\(m-1\ne0\Leftrightarrow m\ne1\Rightarrow\Delta'< 0\Leftrightarrow\left(-m\right)^2-\left(m-2\right)\left(m-1\right)< 0\Leftrightarrow m< \dfrac{2}{3}\)
\(c,\left(2-m\right)x^2-2\left(m+1\right)x+4-m=0\)
\(2-m=0\Leftrightarrow m=2\Rightarrow-6x+2=0\Leftrightarrow x=\dfrac{1}{3}\left(ktm\right)\)
\(2-m\ne0\Leftrightarrow m\ne2\Rightarrow\Delta'< 0\Leftrightarrow[-\left(m+1\right)]^2-\left(4-m\right)\left(2-m\right)< 0\Leftrightarrow m< \dfrac{7}{8}\)

Pt vô nghiệm khi:
\(\Delta=\left(2m+1\right)^2-\left(5m^2+3m+16\right)< 0\)
\(\Leftrightarrow-m^2+m-15< 0\) (luôn đúng)
Vậy pt đã cho vô nghiệm với mọi m

a: \(\left\{{}\begin{matrix}mx+2y=m+2\\\left(2m-1\right)x+\left(m+1\right)y=2\left(m+1\right)\end{matrix}\right.\)
Khi m=3 thì hệ sẽ là:
3x+2y=5 và 5x+4y=8
=>x=2 và y=-1/2
b: Hệ có nghiệm duy nhất thì \(\dfrac{m}{2m-1}< >\dfrac{2}{m+1}\)
=>m^2+m<>4m-2
=>m^2-3m+2<>0
=>m<>1 và m<>2
hệ có vô số nghiệm thì \(\dfrac{m}{2m-1}=\dfrac{2}{m+1}=\dfrac{2}{2\left(m+1\right)}=\dfrac{1}{m+1}\)
=>m/2m-1=2/m+1 và 2/m+1=1/m+1(vô lý)
=>Ko có m thỏa mãn
Để hệ vô nghiệm thì m/2m-1=2/m+1<>1/m+1
=>m=2 hoặc m=1

1) Thay m=2 vào (1), ta được:
\(x^2-2\cdot3x+16-8=0\)
\(\Leftrightarrow x^2-6x+8=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\)
Vậy: Khi m=2 thì (1) có hai nghiệm phân biệt là: \(x_1=2\); \(x_2=4\)
b) Ta có: \(\Delta=4\cdot\left(2m-1\right)^2-4\cdot1\cdot\left(8m-8\right)\)
\(\Leftrightarrow\Delta=4\cdot\left(4m^2-4m+1\right)-4\left(8m-8\right)\)
\(\Leftrightarrow\Delta=16m^2-16m+4-32m+32\)
\(\Leftrightarrow\Delta=16m^2-48m+36\)
\(\Leftrightarrow\Delta=\left(4m\right)^2-2\cdot4m\cdot6+6^2\)
\(\Leftrightarrow\Delta=\left(4m-6\right)^2\)
Để phương trình có hai nghiệm phân biệt thì \(\left(4m-6\right)^2>0\)
mà \(\left(4m-6\right)^2\ge0\forall m\)
nên \(4m-6\ne0\)
\(\Leftrightarrow4m\ne6\)
hay \(m\ne\dfrac{3}{2}\)
Vậy: Để phương trình có hai nghiệm phân biệt thì \(m\ne\dfrac{3}{2}\)