Cho hình vuông ABCD. MN song song với BD. Biết MN = 7 cm, BD=10 cm. Tính diện tích hình thang DNMB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 5 2019
Bn tự vẽ hình nhé !
Độ dài chiều cao AB là :
40 + 10 = 50 ( cm )
Diện tích ABCD là :
( 50 + 60 ) x 50 : 2 = 2750 ( cm2 )
Diện tích NCD là :
60 x 10 : 2 = 300 ( cm2 )
Diện tích ANB là :
50 x 40 : 2 = 1000 ( cm2 )
Diện tích ADN là :
2750 - 300 - 1000 = 1450 ( cm2 )
Độ dài cạnh MN là :
1450 x 2 : 50 = 58 ( cm )
=> diện tích ABMN là : ( 50 + 58 ) x 40 : 2 = 2160 ( cm2 )
Đ/S : 2160 cm2
Tk mk nha
T
31 tháng 5 2019
#)Giải :
#)Giải :
Độ dài chiều cao AD = 40 + 10 = 50 ( cm )
\(S_{ABCD}=\frac{\left(50+60\right)x50}{2}=2750\left(cm^2\right)\)
\(S_{NCD}=\frac{60x10}{2}=300\left(cm^2\right)\)
\(S_{ANB}=\frac{50x40}{2}=1000\left(cm^2\right)\)
\(S_{AND}=2750-300-1000=1450\left(cm^2\right)\)
Độ dài cạnh \(MN=\frac{1450x2}{50}=58\left(cm\right)\)
\(\Rightarrow S_{ABMN}=\frac{\left(50+58\right)x40}{2}=2160\left(cm^2\right)\)
Đ/số : .......................
#~Will~be~Pens~#
A
11 tháng 4 2022
Độ dài cạnh AD là :
40 + 10 = 50(cm)
Diện tích hình thang ABCD là :
( 50 + 60 ) × 50 : 2 = 2750(cm2)
Diện tích tam giác ANB là :
50 × 40: 2 = 1000 (cm2)
Diện tích tam giác NCD là :
60 × 10 : 2 = 300(cm2)
Diện tích tam giác AND là :
2750 − 100 − 300 = 1450(cm2)
Độ dài cạnh MN là :
1450 × 2 : 50 = 58(cm)
Diện tích hình thang MNCD là :
(50 + 58) × 40 : 2 = 2160(cm2)
Đáp số : 2160cm2
CH
Cô Hoàng Huyền
Admin
VIP
8 tháng 3 2018
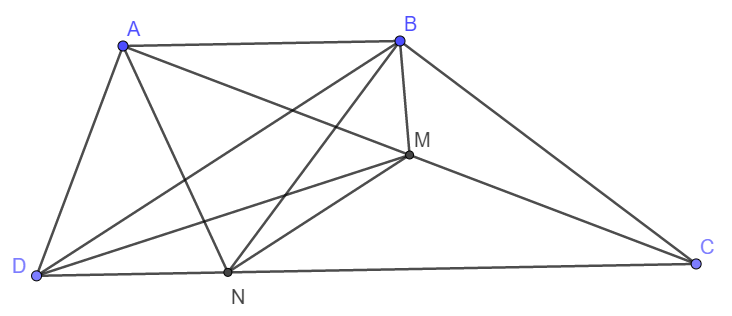
a) Ta thấy hai tam giác MN và DMN có chung cạnh MN.
Lại có do DB // MN nên chiều cao hà từ B và D xuống MN là bằng nhau.
Vậy diện tích tam giác BNM bằng diện tích tam giác DMN.
b) Ta thấy \(AM=MC\Rightarrow\frac{S_{ABM}}{S_{BAC}}=\frac{1}{2};\frac{S_{ADM}}{S_{DAC}}=\frac{1}{2}\)
Vậy nên \(\frac{S_{ABM}+S_{ADM}}{S_{BAC}+S_{DAC}}=\frac{1}{2}\Rightarrow\frac{S_{ABMD}}{S_{ABCD}}=\frac{1}{2}\)
\(\Rightarrow S_{ABMD}=16:2=8\left(cm^2\right)\)
Lại có \(S_{ABMD}=S_{ABMND}-S_{DMN}=S_{ABND}+S_{BMN}-S_{DMN}\)
\(=S_{ABND}\) hay \(S_{ABND}=8cm^2\)
CH
Cô Hoàng Huyền
Admin
VIP
8 tháng 3 2018
Em tham khảo tại link dưới đây nhé.
Câu hỏi của Nguyễn Lê Hoàng - Toán lớp 5 - Học toán với OnlineMath
giúp mình với