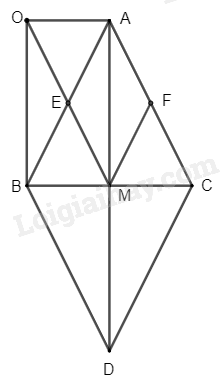
cho tam giác ABC cân tại A.Gọi D,E,F lần lượt là trung điểm của AB,AC,BC 1>lấy K đối xứng với F qua D , chứng minh AFBK À hình chữ nhật 2>Gọi O là dao điểm của EK và AD , H là gia điểm của DF và BE . Chứng minh 1>tứ giác AKDE là hình bình hành 2>HO vuông góc DE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 12 2021
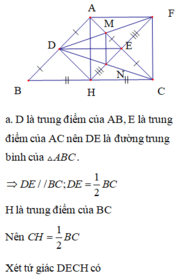
a: Xét ΔABC có
D là tđiểm của AB
E là tđiểm của AC
Do đó: DE là đường trung bình
=>DE//FC và DE=FC
hay DECF là hình bình hành
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
a) Xét tứ giác \(ABDC\) có:
\(M\) là trung điểm của \(BC\) (gt)
\(M\) là trung điểm của \(AD\) (do \(D\) đối xứng với \(A\) qua \(BC\))
Suy ra \(ABDC\) là hình bình hành
b) Do \(\Delta ABC\) cân tại \(A\), có \(AM\) là trung tuyến (gt)
Suy ra \(AM\) là đường cao, trung trực, phân giác
Suy ra \(AM\) vuông góc \(BM\) và \(CM\)
Xét tứ giác \(OAMB\) ta có:
\(E\) là trung điểm của \(OM\) và \(AB\) (gt)
Suy ra \(OAMB\) là hình bình hành
Suy ra \(OB\) // \(AM\); \(OA\) // \(MB\); \(OA = BM\); \(OB = AM\)
Mà \(AM \bot BM\) (cmt)
Suy ra: \(AM \bot OA\); \(OB \bot MB\)
Mà \(AM\) // \(OB\) (cmt)
Suy ra \(OB \bot OA\)
Xét \(\Delta AOB\) và \(\Delta MBO\) (các tam giác vuông) ta có:
\(\widehat {{\rm{AOB}}} = \widehat {{\rm{OBM}}} = 90^\circ \)
\(AO = MB\) (cmt)
\(OB = AM\) (cmt)
Suy ra \(\Delta AOB = \Delta MBO\) (c-g-c)
Suy ra \(OM = AB\)
c) \(OM = AB\) (cmt)
Mà \(EM = EO = \frac{1}{2}OM\); \(EA = EB = \frac{1}{2}AB\)
Suy ra \(EO = EA = EM = EB\) (1)
Xét \(\Delta ABC\) cân ta có: \(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) và \(AB = AC\)
Mà \(EA = EB = \frac{1}{2}AB\); \(FA = FC = \frac{1}{2}AC\) (gt)
Suy ra \(AE = EB = FA = FM\) (2)
Xét \(\Delta BEM\) và \(\Delta CMF\) ta có:
\(BE = CF\) (cmt)
\(\widehat {{\rm{ABC}}} = \widehat {{\rm{ACB}}}\) (cmt)
\(BM = CM\) (gt)
Suy ra \(\Delta BEM = \Delta CFM\) (c-g-c)
Suy ra \(EM = FM\) (3)
Từ (1), (2), (3) suy ra \(AE = AF = FM = ME\)
Suy ra \(AEMF\) là hình thoi
20 tháng 1 2022
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của BC
Do đó: DE là đường trung bình
=>DE//AC
hay DACE là hình thang
b: Xét tứ giác AFCE có
K là trung điểm của AC
K là trung điểm của FE
Do đó: AFCE là hình bình hành
mà \(\widehat{AEC}=90^0\)
nên AFCE là hình chữ nhật
9 tháng 12 2021
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của BC
Do đó: DE là đường trung bình của ΔABC
1: Xét tứ giác AFBK có
D là trung điểm chung của AB và FK
góc AFB=90 độ
=>AFBK là hình chữ nhật
2: Xét ΔBAC có
BF/BC=BD/BA
nên DF//AC và DF=AC/2
=>DF//AE và DF=AE
=>DK//AE và DK=AE
=>AKDE là hình bình hành
=>AD cắt KE tại trung điểm của mỗi đường
=>O là trung điểm chung của AD và KE
2: Xét ΔABC có AD/AB=AE/AC
nên DE//BC và DE=BC/2
=>DE//BF và DE=BF
=>DEFBlà hình bình hành
=>DF cắt EB tại trung điểm của mỗi đường
=>H là trung điểm chung của FD và EB
Xét ΔEKB có EO/EK=EH/EB
nên OH//KB
=>OH vuông góc BC
=>OH vuông góc DE