cho tam giác ABC có AD là tia phân giác của góc A, AB=5cm, AC=7cm, BC=6cm tính độ dài đoạn BD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
5 tháng 2 2020
a) Theo tính chất đường phân giác ta có:
\(\frac{AD}{DC}=\frac{BA}{BC}\) => \(\frac{AD}{AD+DC}=\frac{BA}{BA+BC}\) (tính chất dãy tỉ số bằng nhau)
Suy ra: \(\frac{AD}{AC}=\frac{BA}{BA+BC}\) => \(\frac{AD}{6}=\frac{5}{5+7}\) => AD = 2,5.
b) Xét tam giác ABD có AO là phân giác. Suy ra: \(\frac{OB}{OD}=\frac{AB}{AD}=\frac{5}{2,5}=2\)
Xét tam giác BDM có: \(\frac{OB}{OD}=2\), \(\frac{GB}{GM}=2\) (theo tính chất trọng tâm).
Suy ra \(\frac{OB}{OD}=\frac{GB}{GM}\) (cùng bằng 2) => OG // DM (theo định lý Ta-let đảo)
Vậy OG//AC
27 tháng 2 2021
a) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{6}{4.5}=\dfrac{8}{BD}\)
\(\Leftrightarrow BD=\dfrac{8\cdot4.5}{6}=\dfrac{36}{6}=6\left(cm\right)\)
Vậy:BD=6cm
b) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{AB}{BD}=\dfrac{AC}{CD}\)(Tính chất đường phân giác của tam giác)
\(\Leftrightarrow\dfrac{8}{BD}=\dfrac{6}{CD}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{8}{BD}=\dfrac{6}{CD}=\dfrac{8+6}{BD+CD}=\dfrac{14}{BD}=\dfrac{14}{7}=2\)
Do đó:
\(\dfrac{6}{CD}=2\)
hay CD=3(cm)
Vậy: CD=3cm
31 tháng 1 2016
GIẢI.
Xét tam giác ABC, có : AE tia phân giác của góc BAC (gt)
=>\(\frac{EB}{EC}=\frac{AB}{AC}\) hay \(\frac{EB}{AB}=\frac{EC}{AC}\)
Áp dụng tính chất dãy tỉ lệ thức :
\(\frac{EB}{AB}=\frac{EC}{AC}=\frac{EB+EC}{AB+AC}=\frac{BC}{AB+AC}=\frac{7}{11}\)
=>EB =\(\frac{5.7}{11}\) =3,18cm.
=>EC =\(\frac{6.7}{11}\) =3,82cm.
ZR
31 tháng 1 2016
AE là đường phân giác của tam giác ABC nên
\(\frac{AE}{AB}=\frac{EC}{AC}\)
Áp dụng tính chất tỉ lệ thức
\(\frac{AE}{AB}=\frac{EC}{AC}=\frac{EB+EC}{AB+AC}=\frac{BC}{AB+AC}\)
\(\Rightarrow EB=\frac{AB.BC}{AB+AC}=\frac{5.7}{5+6}\)
EC = BC- BE ≈ 3,8
- See more at: http://toanhocviet.com/tinh-chat-duong-phan-giac-cua-tam-giac_n59185_g790.aspx#sthash.odDjd4Z7.dpuf
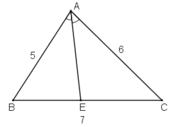
vi AD là tia phân giác góc A của tam giác ABC nên:
BD/AB = DC/AC
hay BD/5 = DC/7 = (BD + DC)/5+7 = 1/2
do đó DB = 5/2