Question

[Buddy]

Dùng một thước có ĐCNN là 1 mm và một đồng hồ đo thời gian có ĐCNN 0,01s để đo 5 lần thời gian chuyển động của chiếc xe đồ chơi chạy bằng pin từ điểm A (vA = 0) đến điểm B (Hình 3.1). Ghi các giá trị vào Bảng 3.1 và trả lời các câu hỏi.

a) Nguyên nhân nào gây ra sự sai khác giữa các lần đo?

b) Tính sai số tuyệt đối của phép đo s, t và điền vào Bảng 3.1.

c) Viết kết quả đo:

s = …..; t = …..

d) Tính sai số tỉ đối:

δ_t = \(\dfrac{\Delta t}{\overline{t}}\).100% =...; δ_s = \(\dfrac{\Delta s}{\overline{s}}\).100% =...

δ_v = ...; Δ_v = ...

Answer 1

[Hà Quang Minh]

Answer 2

[Quoc Tran Anh Le]

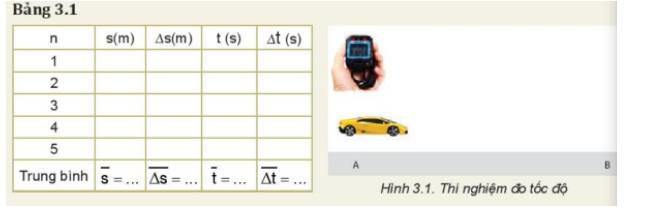
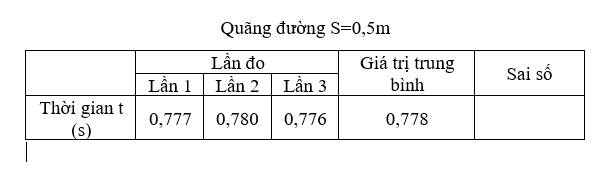
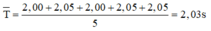
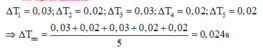
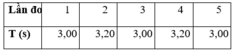
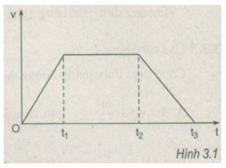
a) Nguyên nhân gây ra sự sai khác giữa các lần đo là:

- Do đặc điểm và cấu tạo của dụng cụ đo

- Do điều kiện làm thí nghiệm chưa được chuẩn

- Do thao tác khi đo

b) Ta có:

\(\overline {\Delta s}  = \frac{{\left| {\overline s  - {s_1}} \right| + \left| {\overline s  - {s_2}} \right| + ... + \left| {\overline s  - {s_5}} \right|}}{5} = 0,00168\)

\(\overline {\Delta t}  = \frac{{\left| {\overline t  - {t_1}} \right| + \left| {\overline t  - {t_2}} \right| + ... + \left| {\overline t  - {t_5}} \right|}}{5} = 0,0168\)

c) Viết kết quả đo:

Ta có:

\(\Delta s = \overline {\Delta s}  + \Delta {s_{dc}} = 0,00168 + \frac{{0,001}}{2} = 0,00218\)

\(\Delta t = \overline {\Delta t}  + \Delta {t_{dc}} = 0,0168 + \frac{{0,01}}{2} = 0,0218\)

Suy ra:

\(s = \overline s  \pm \Delta s = 0,6514 \pm 0,00218\left( m \right)\)

\(t = \overline t  \pm \Delta t = 3,514 \pm 0,0218\left( s \right)\)

d) Tính sai số tỉ đối:

\(\delta t = \frac{{\Delta t}}{{\overline t }}.100\%  = \frac{{0,0218}}{{3,514}}.100\%  = 0,620\)

\(\delta s = \frac{{\Delta s}}{{\overline s }}.100\%  = \frac{{0,00218}}{{0,6514}}.100\%  = 0,335\)

\(\delta v = \frac{{\Delta s}}{{\overline s }}.100\%  + \frac{{\Delta t}}{{\overline t }}.100\%  = 0,335 + 0,620 = 0,955\)

\(\Delta v = \delta v.\overline v  = 0,955.\frac{{0,6514}}{{3,514}} = 0,177\left( {m/s} \right)\)