x2.y+x.y-x=4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
x2y + xy - x = 6
x2y + xy - x -1 = 5
xy.(x + 1) - (x + 1) = 5
(x = 1).(xy - 1) = 1.5 = (-1).(-5) = 5.1 = (-5).(-1)
Ta có bảng giá trị;
| x+1 | 1 | -1 | 5 | -5 |
| x | 0 | -2 | 4 | -6 |
| xy - 1 | / | -5 | / | -1 |
| y | / | 2 | / | 0 |
Vậy (x;y) = (-2;2) ; (-6;0)


Ta có: 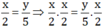 (Nhân cả hai vế của đẳng thức với
(Nhân cả hai vế của đẳng thức với 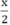 ).
).
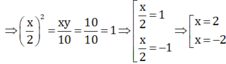
TH1 : Nếu x = -2 ⇒ y = -5
TH2 : Nếu x = 2 ⇒ y = 5
Cách 2:
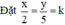
⇒ x = 2k; y = 5k.
Ta có: x.y = 10 ⇒ 2k.5k = 10 ⇒ 10k2 = 10 ⇒ k2 = 1 ⇒ k = 1 hoặc k = -1.
+ Nếu k = 1 thì x = 2k = 2; y = 5k = 5.
+ Nếu k = -1 thì x = 2k = -2; y = 5k = -5.
Vậy x = 2 ; y = 5 hoặc x = -2; y = -5.


b) \(xy+3x-2y=11\)
\(xy+3x-2y-6=11-6\)
\(xy+3x-2y-6=5\)
\(\left(xy+3x\right)-\left(2y+6\right)=5\)
\(x\left(y+3\right)-2\left(y+3\right)=5\)
\(\left(x-2\right)\left(y+3\right)=5\)
\(\Rightarrow5=\left(-1\right)\left(-5\right)=1\cdot5\)
Bạn tự lập bảng mà thử nghiệm nhé

\(x^2\cdot y+x\cdot y-x=4\)
\(x\cdot y\cdot\left(x+1\right)-x=4\)
\(x\cdot y\cdot\left(x+1\right)-x-1=4-1\)
\(xy\cdot\left(x+1\right)-\left(x+1\right)=3\)
\(\left(x+1\right)\left(xy-1\right)=3\)
⇒ \((x + 1) ; (xy - 1)\) là ước của 3
⇒ \(\text{(x + 1) ; (xy - 1)}\in\left\{\pm1;\pm3\right\}\)
Ta có:
TH1:
\(\left[{}\begin{matrix}x+1=1\\xy-1=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1-1\\xy=3+1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\xy=4\end{matrix}\right.\Rightarrow y=\dfrac{xy}{x}=\dfrac{4}{0}\) (vô nghiệm)
TH2:
\(\left[{}\begin{matrix}x+1=-1\\xy-1=-3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-1-1\\xy=-3+1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-2\\xy=-2\end{matrix}\right.\)\(\Rightarrow y=\dfrac{xy}{x}=\dfrac{-2}{-2}=1\) (chọn)
TH3:
\(\left[{}\begin{matrix}x+1=3\\xy-1=1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=3-1\\xy=1+1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\xy=2\end{matrix}\right.\)\(\Rightarrow y=\dfrac{xy}{x}=\dfrac{2}{2}=1\) (chọn)
TH4:
\(\left[{}\begin{matrix}x+1=-3\\xy-1=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-3-1\\xy=-1+1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=-4\\xy=0\end{matrix}\right.\)\(\Rightarrow y=\dfrac{xy}{x}=\dfrac{0}{-4}=0\)(vô nghiệm)
Vậy (x,y)ϵ{(-2 ; 1);(2 ; 1)}