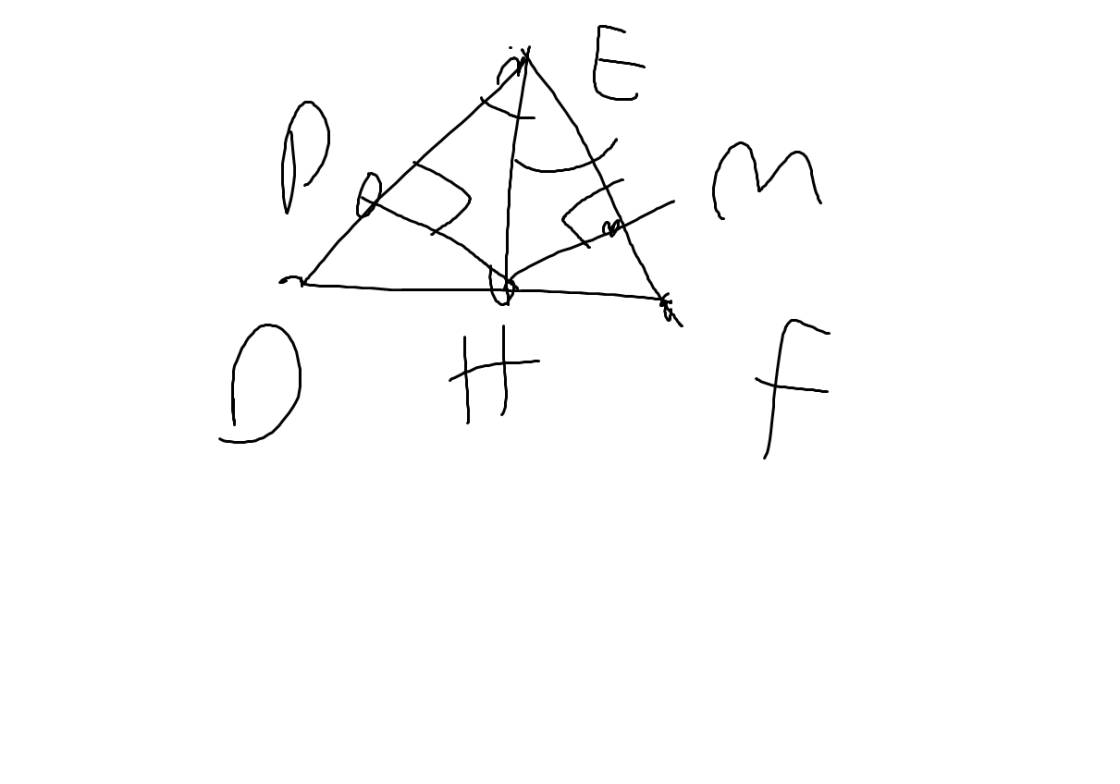
Cho DEF vuông tại E, đường cao EH. Cho biết DE = 15 cm và EF = 20 cm. a) Chứng minh rằng: EH. DF = ED. EF. Tính DF; EH. b) Kẻ HM vuông góc ED , HN vuông góc EF , Chứng minh tam giác EMN ~ EDF
c) trung tuyến EK của tam giác DEF cắt MN tại I , tính diện tích tam giác EIM ?