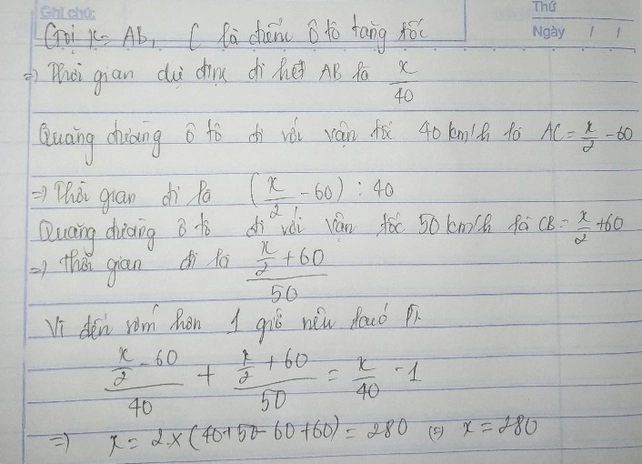giải bài toán này bằng cách lập phương trình hộ mk vs ạ :
.Một ô tô dự định đi từ A đến B với vận tốc là 50km/h nhưng khi đi được 2/3 quãng đường thì ô tô tăng vận tốc thêm 10km và ô tô đó đến B sớm hơn dự định là 24 phút . Tính quãng đường AB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AT
17 tháng 8 2016
Gọi thời gian dự định đi hết quãng đường là x.
Độ dài quãng đường AB là: S = v.t = 40x
Nửa quãng đường là S/2 = 40x/2 = 20x.
Nửa quãng đường đầu đi vs vtốc dự định (40km/h)
=> Thời gian đi hết nửa quãng đường đầu là: t1 = S : v1 = 20x : 40 = 1/2x
Nửa quãng đường đầu đi vs vtốc tăng hơn dự định 10km/h (50km/h)
=> Thời gian đi hết nửa quãng đường sau là t2 = S : v2 = 20x : 50 = 2/5x
Tổng thời gian đi hết quãng đường là: t = t1 + t2 = 1/2x + 2/5x = 9/10x
Do thực tế đến B sớm hơn dự kiến 1h nên ta có: x - 9/10x = 1 => x = 10 (h)
=> Độ dài quãng đường AB là S = 40.10 = 400 (km).
31 tháng 7 2023
Gọi độ dài quãng đường AB là x
Thời gian dự định là x/50
Trong 2h, xe đi được 50*2=100km
Theo đề, ta có phương trình:
\(\dfrac{x}{50}=\dfrac{7}{3}+\dfrac{x-100}{60}\)
=>x/50-x/60+5/3=7/3
=>x/300=2/3
=>x=200
29 tháng 1
Gọi vận tốc ban đầu của ô tô là x(km/h)
Thời gian dự kiến ban đầu sẽ đi hết quãng đường là \(\dfrac{840}{x}\left(giờ\right)\)
Thời gian đi nửa quãng đường đầu tiên là \(\dfrac{840}{2x}=\dfrac{420}{x}\left(giờ\right)\)
Vận tốc lúc sau là x+2(km/h)
Thời gian đi hết quãng đường còn lại là \(\dfrac{420}{x+2}\left(giờ\right)\)
30p=0,5h=1/2h
Theo đề, ta có phương trình:
\(\dfrac{420}{x}+\dfrac{420}{x+2}+\dfrac{1}{2}=\dfrac{840}{x}\)
=>\(-\dfrac{420}{x}+\dfrac{420}{x+2}=\dfrac{-1}{2}\)
=>\(\dfrac{-420x-840+420x}{x\left(x+2\right)}=\dfrac{-1}{2}\)
=>\(x\left(x+2\right)=1680\)
=>\(x^2+2x-1680=0\)
=>(x-40)(x+42)=0
=>\(\left[{}\begin{matrix}x-40=0\\x+42=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=40\left(nhận\right)\\x=-42\left(loại\right)\end{matrix}\right.\)
vậy: vận tốc dự định là 40km/h
24 tháng 1
Gọi độ dài quãng đường AB là x(km)
(Điều kiện: x>0)
Thời gian dự định đi hết quãng đường AB là \(\dfrac{x}{50}\left(giờ\right)\)
Trong 2h ô tô đi được \(2\cdot50=100\left(km\right)\)
Độ dài quãng đường còn lại là x-100(km)
Thời gian thực tế ô tô đi hết quãng đường AB là:
\(2+\dfrac{1}{3}+\dfrac{x-100}{50+10}=\dfrac{7}{3}+\dfrac{x-100}{60}\left(giờ\right)\)
Theo đề, ta có phương trình:
\(\dfrac{7}{3}+\dfrac{x-100}{60}=\dfrac{x}{50}\)
=>\(\dfrac{7}{3}+\dfrac{x}{60}-\dfrac{5}{3}=\dfrac{x}{50}\)
=>\(\dfrac{x}{60}-\dfrac{x}{50}=-\dfrac{2}{3}\)
=>\(\dfrac{-x}{300}=\dfrac{-2}{3}\)
=>x=200(nhận)
Vậy: Độ dài quãng đường AB là 200km
2 tháng 6 2017
Gọi quãng đường AB là \(x\left(km\right)\)
Thời gian dự kiến đi hết quãng đường AB là \(x:40\)
Thời gian thực tế xe đi với vận tốc 40 là : \(\frac{0,5x-60}{40}\)
Thời gian xe đi nốt quãng đường AB với vận tốc 50 là :\(\frac{0,5x+60}{50}\)
Xe đến sớm hơn dự kiến 1 giờ nên có :
\(1+\frac{0,5x-60}{40}+\frac{0,5x+60}{50}=\frac{x}{40}\)
\(\Leftrightarrow40.50+50\left(0,5x-60\right)+40\left(0,5x+60\right)=50x\)
\(2000+45x-3000+2400=50x\Leftrightarrow5x=1400\Leftrightarrow x=280\left(km\right)\)