Đồ thị hàm số y=x2 đi qua hai điểm (\(\sqrt{2}\);m)và(-\(\sqrt{3}\);n).Khi đó giá trị của biểu thức m2-n2 bằng
A.5 B.-1 C.1 D.-5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
y = x 2 + 2 x x − 1
Phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số là
y = x 2 + 2 x ' x − 1 ' = 2 x + 2

Đồ thị hàm số đi qua A (-1; 2) nên tọa độ của A nghiệm đúng phương trình hàm số: 2 = a - 1 2 } ⇔ a = 2
Hàm số đã cho: y = 2 x 2
Vẽ đồ thị hàm số: y = 2 x 2
x |
-2 |
-1 |
0 |
1 |
2 |
| y = 2 x 2 | 8 |
2 |
0 |
2 |
8 |
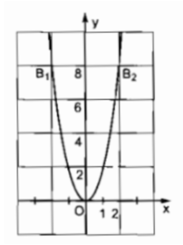

Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}a\cdot\sqrt{2}+b=4-\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\left(\sqrt{2}-2\right)=4-2\sqrt{2}\\2a+b=\sqrt{2}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}a=\dfrac{4-2\sqrt{2}}{\sqrt{2}-2}=-2\\b=\sqrt{2}+4\end{matrix}\right.\)

a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5.
Bài giải:
a) Hàm số đã cho là y = 2x + b.
Vì đồ thị đi qua điểm A(1,5; 0) nên 0 = 2 . 1,5 + b. Suy ra b = -3.
Vậy hàm số đã cho là y = 2x - 3.
b) Hàm số đã cho là y = 3x + b.
Vì đồ thị đi qua điểm A(2; 2) nên 2 = 3 . 2 + b. Suy ra b = -4.
Vậy hàm số đã cho là y = 3x - 4.
c) Vì đồ thị của hàm số đã cho song song với đường thẳng y = √3x nên nó có hệ số góc là a = √3. Do đó hàm số đã cho là y = √3x + b.
Vì đồ thị đi qua điểm B(1; √3 + 5) nên √3 + 5 = √3 . 1 + b. Suy ra b = 5.
Vậy hàm số đã cho là y = √3x + 5
Thay hai điểm `(\sqrt{2};m)` và `(-\sqrt{3};n)` vào `y=x^2` ta có:
`{(m=(\sqrt{2})^2),(n=(-\sqrt{3})^2):}<=>{(m^2=4),(n^2=9):}`
`=>m^2-n^2=4-9=-5`
`->bb D`
Thay hai điểm vào hàm số
\(\Rightarrow\left\{{}\begin{matrix}\sqrt{2}=m^2\\-\sqrt{3}=n^2\end{matrix}\right.\)
\(m^2-n^2=\sqrt{2}-\left(-\sqrt{3}\right)=\sqrt{2}+\sqrt{3}\)