Question

[toi la toi toi la toi]

Cho tam giác ABC cân tại A. Trên tia đối của BA lấy điểm D, trên tia đối của BC lấy điểm E sao cho BD=CE. Gọi K là giao điểm của CD và BE. Chứng minh rằng:  

1) BE=CD.

2) tam giác BKD= tam giác CKE.

3) AK là phân giác của góc A.

4)gọi M,N lần lượt là trung điểm của BC và DE. Chứng minh A,M,K,N thẳng hàng.

Answer 1

[soyeon_Tiểu bàng giải]

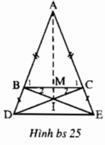
tự vẽ hình nhé!

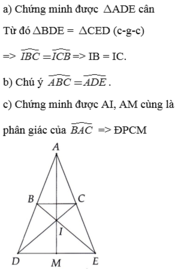
2) \(\Delta AEB=\Delta ADC\left(c.g.c\right)\)

=> \(\widehat{ABE}=\widehat{ACD}\)(2 góc2 t/ứ)

Mà \(\widehat{ABE}+\widehat{EBD}=180^o\)(kề bù)

\(\widehat{ACD}+\widehat{DCE}=180^o\)(kề bù)

Nên \(\widehat{EBD}=\widehat{DCE}\)

\(\Delta BKD=\Delta CKE\left(g.c.g\right)\)(đpcm)

3) \(\Delta BKD=\Delta CKE\)(câu 2) => KD = KE (2 cạnh t/ứ)

\(\Delta AKE=\Delta AKD\left(c.c.c\right)\)\(\Rightarrow\widehat{EAK}=\widehat{DAK}\)(2 góc t/ứ)

=> AK là p/g \(\widehat{BAC}\left(đpcm\right)\)

4) Có: KE = KD (\(\Delta CKE=\Delta BKD\))

=> K cách đều E và D

=> K nằm trên đường trung trực của ED  (2)

Cần c/m \(AM⊥BC;AN⊥ED\)

Mà BC // ED (tự c/m) => A,M,N thẳng hàng  (3)

Có N nằm trên đường trung trực của ED  (4)

Từ (2);(3);(4) => A,M,K,N thẳng hàng (đpcm)

Answer 2

[toi la toi toi la toi]

AI GIÚP MIK DZỚI