CMR: (a+b)2 =a2+2ab+b2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
P
CMR :1,a2+b2=<a+b>2-2ab
2,a3+b3=<a+b>3-3ab.<a+b>
3,a3-b3=<a-b>3+3ab.<a+b>
Cho :a+b=1
Tính :A=a3+b3+3ab
2
16 tháng 8 2021
2
Ta có:
VP=(a+b)3−3ab(a+b)VP=(a+b)3-3ab(a+b)
=a3+b3+3ab(a+b)−3ab(a+b)=a3+b3+3ab(a+b)-3ab(a+b)
=a3+b3=VT(dpcm)
CH
16 tháng 8 2021
1, \(VT=a^2+b^2=a^2+b^2+2ab-2ab=\left(a+b\right)^2-2ab=VP\left(đpcm\right)\)
12 tháng 5 2022
a: \(a^4+b^4\ge2a^2b^2\)
\(\Leftrightarrow a^4-2a^2b^2+b^4>=0\)
hay \(\left(a^2-b^2\right)^2\ge0\)(luôn đúng)
d: \(\left(a+b\right)^2\ge4ab\)
\(\Leftrightarrow a^2+2ab+b^2-4ab\ge0\)
\(\Leftrightarrow\left(a-b\right)^2\ge0\)(luôn đúng)
AD
1
5 tháng 1 2023
(a-b)^2=(a-b)(a-b)=a^2-ab-ab+b^2=a^2-2ba+b^2
(a-b)(a+b)=a^2+ab-ab-b^2=a^2-b^2
(a+3)^3=(a+b)^2*(a+b)
=(a^2+2ab+b^2)(a+b)
=a^3+a^2b+2a^2b+2ab^2+b^2a+b^3
=a^3+3a^2b+3ab^2+b^3
PH
0
CW
18 tháng 7 2016
VT = (a+b+c)^2
= [(a+b) + c]^2
= (a+b)^2 + 2(a+b)c + c^2
= a^2 + 2ab + b^2 + 2ac + 2bc + c^2
= a^2 + b^2 + c^2 + 2ab + 2ac + 2bc = VP
Vậy ...
---------------------------------------
VT= (a+b+c)^2 + a^2 + b^2 + c^2
= [(a+b) + c]^2 + a^2 + b^2 + c^2
= (a+b)^2 + 2(a+b)c + c^2 + a^2 + b^2 + c^2
= a^2 + 2ab + b^2 + 2ac + 2bc + c^2 + a^2 + b^2 + c^2
= (a^2 + 2ab + b^2) + (b^2 + 2bc + c^2) + (c^2 + 2ca + a^2)
= (a+b)^2 + (b+c)^2 + (c+a)^2 = VP
Vậy...
17 tháng 2 2021
a, a(b+c)−b(a−c)a(b+c)−b(a−c)
=ab+ac−(ab−bc)=ab+ac−(ab−bc)
=ab+ac−ab+bc=ab+ac−ab+bc
=ac+bc=ac+bc
=(a+b)c=(a+b)c
b,(a+b)(a−b)(a+b)(a−b)
=(aa+ab)−(ab+bb)=(aa+ab)−(ab+bb)
=aa+ab−ab−bb
7 tháng 1 2018
\(a,\dfrac{2x+2y}{a^2+2ab+b^2}.\dfrac{ax-ay+bx-by}{2x^2-2y^2}\)
\(b,\dfrac{a+b-c}{a^2+2ab+b^2-c^2}.\dfrac{a^2+2ab+b^2+ac+bc}{a^2-b^2}\)
\(=\dfrac{2\left(x+y\right)}{\left(a+b\right)^2}.\dfrac{a\left(x-y\right)+b\left(x-y\right)}{2\left(x^2-y^2\right)}\)
\(=\dfrac{2\left(x+y\right)}{\left(a+b\right)^2}.\dfrac{\left(x-y\right)\left(a+b\right)}{2\left(x-y\right)\left(x+y\right)}\)
\(=\dfrac{1}{a+b}\)
\(b,\dfrac{a+b-c}{a^2+2ab+b^2-c^2}.\dfrac{a^2+2ab+b^2+ac+bc}{a^2-b^2}\)
\(=\dfrac{a+b-c}{\left(a+b\right)^2-c^2}.\dfrac{\left(a+b\right)^2+c\left(a+b\right)}{\left(a-b\right)\left(a+b\right)}\)
\(=\dfrac{a+b-c}{\left(a+b-c\right)\left(a+b+c\right)}.\dfrac{\left(a+b\right)\left(a+b+c\right)}{\left(a-b\right)\left(a+b\right)}\)
\(=\dfrac{1}{a-b}\)
\(c,\dfrac{x^3+1}{x^2+2x+1}.\dfrac{x^2-1}{2x^2-2x+2}\)
\(=\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)^2}.\dfrac{\left(x-1\right)\left(x+1\right)}{2\left(x^2-x+1\right)}\) \(=\dfrac{x-1}{2}\) \(d,\dfrac{x^8-1}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^4\right)^2-1}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^4-1\right)\left(x^4+1\right)}{x+1}.\dfrac{1}{\left(x^2+1\right)\left(x^4+1\right)}\) \(=\dfrac{\left(x^2+1\right)\left(x^2-1\right)}{x+1}.\dfrac{1}{x^2+1}\) \(=\dfrac{\left(x-1\right)\left(x+1\right)}{x+1}\) \(=x-1\) \(e,\dfrac{x-y}{xy+y^2}-\dfrac{3x+y}{x^2-xy}.\dfrac{y-x}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{3x+y}{x\left(x-y\right)}.\dfrac{-\left(x-y\right)}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{3x+y}{x}.\dfrac{-1}{x+y}\) \(=\dfrac{x-y}{y\left(x+y\right)}-\dfrac{-3x-y}{x\left(x+y\right)}\) \(=\dfrac{x\left(x-y\right)+y\left(3x+y\right)}{xy\left(x+y\right)}\) \(=\dfrac{x^2-xy+3xy+y^2}{xy\left(x+y\right)}\) \(=\dfrac{x^2+2xy+y^2}{xy\left(x+y\right)}\) \(=\dfrac{\left(x+y\right)^2}{xy\left(x+y\right)}=\dfrac{x+y}{xy}\)19 tháng 2 2018
tìm giá trị của m để pt 2x-m=1-x nhận giá trị x=-2 là nghiệm
giải hộ e với :)
CM
16 tháng 1 2019
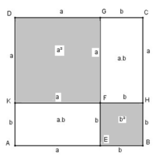
Dựng hình vuông ABCD có cạnh bằng a
Trên cạnh AB lấy điểm E sao cho BE = b
Từ E dựng đường thẳng song song BC cắt CD tại G
Ta có: CG = b, CE = ( a – b ), GD = ( a – b )
Trên cạnh AD lấy điểm K sao cho AK = b
Từ K kẻ đường thẳng song song với AB cắt BC tại H và cắt EG tại F
Ta có: KD = ( a – b ), BH = b
Hình vuông ABCD có diện tích bằng a 2
Hình vuông DKFG có diện tích bằng a - b 2
Hình chữ nhật AEFK có diện tích bằng ( a – b ) b
Hình vuông EBHF có diện tích bằng b 2
Hình chữ nhật HCGF có diện tích bằng ( a – b ).b
S A B C D = S D K F G + S A E F K = S E B H F + S H C G F
nên a - b 2 + a - b b + a - b b + b 2 = a 2
⇒ a - b 2 = a 2 - 2 a b + b 2
PT
2
CM
15 tháng 4 2018
Thay a = -2, b = 4 vào biểu thức ta được:
( − 2 ) 2 + 2. ( − 2 ) .4 + 4 2 − 1 = 4 + ( − 16 ) + 16 − 1 = 3
25 tháng 9 2021
`a^2 + 2ab+b^2-1`
`= (a+b)^2-1`
`=(a+b)^2 - 1^2`
`=(a+b-1)(a+b+1)`
`= (-2+4-1)(-2+4+1)`
`= 3`
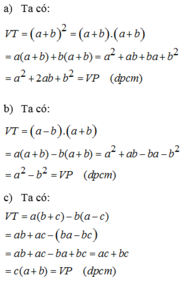
(a+b)2 = (a+b).(a+b) = a.a+a.b+b.a+b.b = a2+ab+ab+b2 = a2+2ab+b2