Trong các khẳng định sau, khẳng định nào sai? A. Một mặt phẳng cắt hai mặt phẳng song song thì hai giao tuyển đó song song. B. Tất cả các mặt của hình hộp đều là hình bình hành. C. Hai mặt phẳng có hai điểm chung 4, F(A = B ) thì chúng có một đường thẳng chung 4 B. duy nhất. D. Tất cả các cạnh bến kéo dài của một hình chóp cụt đồng quy.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn C.
Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Chọn C
Sử dụng hệ quả: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.

Đáp án A
(1) Sai vì ( α ) // a ( β ) // a ( α ) ∩ ( β ) = d ⇒ a / / d tức là có trường hợp chúng cắt nhau.

a)
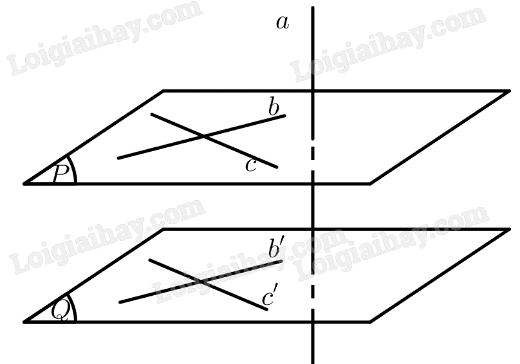
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) song song với nhau và đường thẳng \(a\) vuông góc với \(\left( P \right)\). Ta cần chứng minh \(a \bot \left( Q \right)\).
Trên \(\left( P \right)\) lấy hai đường thẳng \(b,c\) cắt nhau, trên \(\left( Q \right)\) lấy hai đường thẳng \(b',c'\) sao cho \(b'\parallel b,c'\parallel c\).
Vì \(b,c\) cắt nhau nên \(b',c'\) cắt nhau.
\(\begin{array}{l}\left. \begin{array}{l}a \bot \left( P \right) \Rightarrow a \bot b,a \bot c\\b\parallel b',c\parallel c'\end{array} \right\} \Rightarrow a \bot b',a \bot c'\\ \Rightarrow a \bot \left( Q \right)\end{array}\)
b)
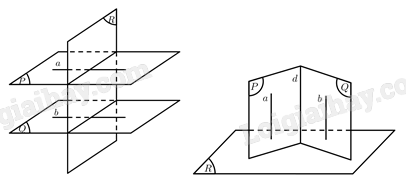
Cho hai mặt phẳng \(\left( P \right),\left( Q \right)\) cùng vuông góc với mặt phẳng \(\left( R \right)\). Ta cần chứng minh \(\left( P \right)\parallel \left( Q \right)\) hoặc \(d \bot \left( R \right)\) với \(d = \left( P \right) \cap \left( Q \right)\).
Vì \(\left( P \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(a \subset \left( P \right)\) sao cho \(a \bot \left( R \right)\), \(\left( Q \right) \bot \left( R \right)\) nên tồn tại đường thẳng \(b \subset \left( Q \right)\) sao cho \(b \bot \left( R \right)\)
\( \Rightarrow a\parallel b\)
Vậy \(\left( P \right)\parallel \left( Q \right)\) hoặc nếu \(\left( P \right),\left( Q \right)\) cắt nhau theo giao tuyến \(d\) thì \(d\parallel a \Rightarrow d \bot \left( R \right)\).
Chọn C