128+(-5).12+(-68):(-17) giúp mik với ạ,cảm ơnn nhìuu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
0
BS
19 tháng 12 2022
\(\dfrac{x+9}{x^2-9}-\dfrac{3}{x^2+3x}\)
\(=\dfrac{x+9}{\left(x-3\right)\left(x+3\right)}-\dfrac{3}{x\left(x+3\right)}\)
\(=\dfrac{x\left(x+9\right)}{x\left(x-3\right)\left(x+3\right)}-\dfrac{3\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+9x-3x+9}{x\left(x-3\right)\left(x+3\right)}\)
\(=\dfrac{x^2+6x+9}{x\left(x-3\right)\left(x+3\right)}=\dfrac{\left(x+3\right)^2}{x\left(x-3\right)\left(x+3\right)}=\dfrac{x+3}{x\left(x-3\right)}\)
______________________________________________________
\(\dfrac{x+1}{2x+6}-\dfrac{x-6}{2x^2+6x}\)
\(=\dfrac{x+1}{2\left(x+3\right)}-\dfrac{x-6}{2x\left(x+3\right)}\)
\(=\dfrac{x\left(x+1\right)}{2x\left(x+3\right)}-\dfrac{x-6}{2x\left(x+3\right)}\)
\(=\dfrac{x^2+x-x+6}{2x\left(x+3\right)}=\dfrac{x^2+6}{2x\left(x+3\right)}\)
15 tháng 1
a: Để A là phân số thì \(n+1\ne0\)
=>\(n\ne-1\)
b: \(n^2-1=0\)
=>\(n^2=1\)
=>\(\left[{}\begin{matrix}n=1\left(nhận\right)\\n=-1\left(loại\right)\end{matrix}\right.\)
Thay n=1 vào A, ta được:
\(A=\dfrac{3\cdot1-1}{1+1}=\dfrac{3-1}{2}=1\)
c: Để A là số nguyên thì \(3n-1⋮n+1\)
=>\(3n+3-4⋮n+1\)
=>\(-4⋮n+1\)
=>\(n+1\in\left\{1;-1;2;-2;4;-4\right\}\)
=>\(n\in\left\{0;-2;1;-3;3;-5\right\}\)
d: \(A=\dfrac{3n-1}{n+1}=\dfrac{3n+3-4}{n+1}=3-\dfrac{4}{n+1}\)
Để A min thì \(\dfrac{-4}{n+1}\) min
=>n+1 là số nguyên dương nhỏ nhất
=>n+1=1
=>n=0
=>\(A=3-\dfrac{4}{0+1}=3-4=-1\)
giúp e với ạ e cảm ơnn
7 tháng 8 2021
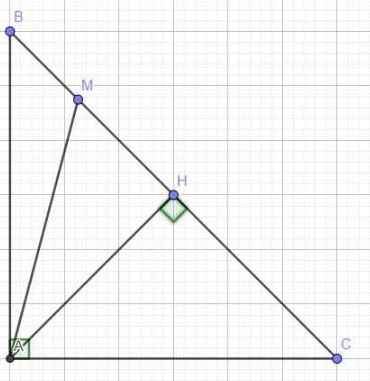
a)Kẻ AH⊥BC
Vì ΔABC vuông cân tại A
⇒ AH cũng là đường trung tuyến
⇒ AH=BH=CH
Ta có:MB2 + MC2 = (BH-HM)2 + (CH+HM)2 = (AH-HM)2+(AH+HM)2
= AH2-2.AH.HM+HM2+AH2+2.AH.HM+HM2=2(AH2+HM2)
Áp dụng định lý Py-ta-go vào ΔAHM vuông tại A ta có:
MA2 = AH2+HM2
⇒ MB2+MC2=2MA2
b) Ta có: MA≥AH (đường xiên và đường vuông góc)
⇒ MA2 ≥ AH2
⇒ 2MA2 ≥ 2AH2
⇒ MB2+MC2 ≥ 2AH2
Dấu "=" xảy ra ⇔ MA=AH ⇔ M là trung điểm của BC
Vậy Min K = 2AH2 ⇔ M là trung điểm của BC
DT
Đỗ Thanh Hải
CTVVIP
6 tháng 10 2021
1 played the piano for 4 years
2 5 years since my father last went to HN
3 been reading a newspaprt for 2 hours
4 have written to her for 4 years
5 is over a years since I last went to see them
6 not rained for 2 weeks
7 kept a diary for 5 years
8 gone swimming since 2001
9 studied E since I was 10 years old
10 saw Tom when he moved to London
AT
5 tháng 7 2021
i) \(\sqrt{3+2\sqrt{2}}+\sqrt{\left(\sqrt{2}-2\right)^2}=\sqrt{\left(\sqrt{2}\right)^2+2.\sqrt{2}.1+1^2}+\left|\sqrt{2}-2\right|\)
\(=\sqrt{\left(\sqrt{2}+1\right)^2}+2-\sqrt{2}=\left|\sqrt{2}+1\right|+2-\sqrt{2}=\sqrt{2}+1+2-\sqrt{2}=3\)
k) \(\sqrt{4-\sqrt{15}}-\sqrt{4+\sqrt{15}}+\sqrt{6}=\sqrt{\dfrac{8-2\sqrt{15}}{2}}-\sqrt{\dfrac{8+2\sqrt{15}}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}\right)^2-2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}\right)^2+2.\sqrt{5}.\sqrt{3}+\left(\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\sqrt{\dfrac{\left(\sqrt{5}-\sqrt{3}\right)^2}{2}}-\sqrt{\dfrac{\left(\sqrt{5}+\sqrt{3}\right)^2}{2}}+\sqrt{6}\)
\(=\dfrac{\left|\sqrt{5}-\sqrt{3}\right|}{\sqrt{2}}-\dfrac{\left|\sqrt{5}+\sqrt{3}\right|}{\sqrt{2}}+\sqrt{6}\)
\(=\dfrac{\sqrt{5}-\sqrt{3}}{\sqrt{2}}-\dfrac{\sqrt{5}+\sqrt{3}}{\sqrt{2}}+\sqrt{6}=\dfrac{-2\sqrt{3}}{\sqrt{2}}+\sqrt{6}=-\sqrt{6}+\sqrt{6}=0\)
m) \(2\sqrt{56}-14\sqrt{\dfrac{2}{7}}+\left(\sqrt{7}-\sqrt{2}\right)\sqrt{7}-\dfrac{8\sqrt{2}}{\sqrt{3}-\sqrt{7}}\)
\(=2\sqrt{4.14}-2\sqrt{49.\dfrac{2}{7}}+7-\sqrt{14}+\dfrac{8\sqrt{2}.\left(\sqrt{7}+\sqrt{3}\right)}{\left(\sqrt{7}-\sqrt{3}\right)\left(\sqrt{7}+\sqrt{3}\right)}\)
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}+\dfrac{8.\left(\sqrt{14}+\sqrt{6}\right)}{4}\)
\(=\sqrt{14}+7+2\left(\sqrt{14}+\sqrt{6}\right)=7+3\sqrt{14}+2\sqrt{6}\)
AH
Akai Haruma
Giáo viên
5 tháng 7 2021
Lời giải:
i.
\(=\sqrt{(\sqrt{2}+1)^2}+|\sqrt{2}-2|=|\sqrt{2}+1|+|\sqrt{2}-2|=\sqrt{2}+1+2-\sqrt{2}=3\)
k.
\(=\frac{1}{\sqrt{2}}(\sqrt{8-2\sqrt{15}}-\sqrt{8+2\sqrt{15}}+\sqrt{12})\)
\(=\frac{1}{\sqrt{2}}(\sqrt{(\sqrt{3}-\sqrt{5})^2}-\sqrt{(\sqrt{3}+\sqrt{5})^2}+2\sqrt{3})\)
\(=\frac{1}{\sqrt{2}}(|\sqrt{3}-\sqrt{5}|-|\sqrt{3}+\sqrt{5}|+2\sqrt{3})=\frac{1}{\sqrt{2}}(-2\sqrt{3}+2\sqrt{3})=0\)
m.
\(=4\sqrt{14}-2\sqrt{14}+7-\sqrt{14}-\frac{8\sqrt{2}(\sqrt{3}+\sqrt{7})}{(\sqrt{3}-\sqrt{7})(\sqrt{3}+\sqrt{7})}\)
\(=\sqrt{14}+7-\frac{8(\sqrt{14}+\sqrt{6})}{-4}=\sqrt{14}+\sqrt{7}+2(\sqrt{14}+\sqrt{6})=3\sqrt{14}+\sqrt{7}+2\sqrt{6}\)
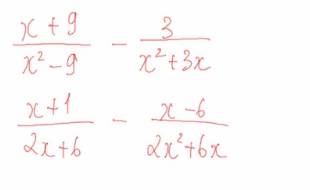
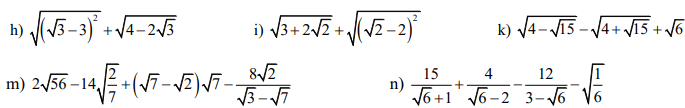
\(128+\left(-5\right).12+\left(-68\right):\left(-17\right)=128+\left(-60\right)+4=68+4=72\)
\(128+\left(-5\right)\cdot12+\left(-68\right):\left(-17\right)\)
\(=128+\left(-60\right)+4=68+4=72\)