Giải giúp với cảm ơn nhiều nha
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
0
N
0
TH
1
4 tháng 3 2022
Bài 1:
Xét ΔDEF có
M là trung điểm của DE
P là trung điểm của DF
Do đó: MP là đường trung bình
=>MP//EF
=>ΔDMP\(\sim\)ΔDEF
Xét ΔDEF có
M là trung điểm của ED
N là trung điểm của FE
Do đó: MN là đường trung bình
=>ΔEMN\(\sim\)ΔEDF
Xét ΔDEF có
P là trung điểm của DF
N là trung điểm của EF
Do đó: PN là đường trung bình
=>PN//DE
hay ΔFPN\(\sim\)ΔFDE
Mọi người giúp mình với, giải chi tiết (+giải thích giúp mình nha), cảm ơn mọi người rất nhiều lun =)
TA
1
L
16 tháng 10 2021
a) bạn tự vẽ đi nhé (cách vẽ RntRbntAmpe)
b)
i)khi ampe kế chỉ 0.3 (A)
Ir=Ib=Ia=0.3(A)
⇒Rtđ =\(\dfrac{U}{Ia}\)=\(\dfrac{12}{0.3}\)=40Ω
khi ampe kế chỉ 0.8
Ir=Ib=Ia=0.8A
=>Rtđ =\(\dfrac{12}{0.8}\)=15Ω
ii) vì R tỉ lệ nghịch với I
=>để Rb max<=>I=0.3A
=>Ir=Ib =0.3 A
có \(\dfrac{Rr}{Rb}=\dfrac{Ib}{Ir}=\dfrac{0.3}{0.3}=1\)
mà từ i) ta có Rtđ =Rr+Rb =40
=> Rr = Rbmax = \(\dfrac{40}{2}\)=20Ω
VV
1
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Phương trình đường thẳng d' qua M và vuông góc \(\Delta\) (nên nhận \(\left(1;1\right)\) là 1 vtpt) có dạng:
\(1\left(x-3\right)+1\left(y-2\right)=0\Leftrightarrow x+y-5=0\)
Gọi H là giao điểm d' và \(\Delta\Rightarrow\) tọa độ H là nghiệm:
\(\left\{{}\begin{matrix}x-y=0\\x+y-5=0\end{matrix}\right.\) \(\Rightarrow H\left(\dfrac{5}{2};\dfrac{5}{2}\right)\)
M' là ảnh của M qua phép đối xứng trục \(\Rightarrow\) H là trung điểm MM'
\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_H-x_M=2\\y_{M'}=2y_H-y_M=3\end{matrix}\right.\) \(\Rightarrow M'\left(2;3\right)\)
Gọi \(d_1\) là ảnh của d qua phép đối xứng trục
Gọi A là giao điểm d và \(\Delta\Rightarrow A\in d_1\), tọa độ A thỏa mãn:
\(\left\{{}\begin{matrix}x+4y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow A\left(\dfrac{3}{5};\dfrac{3}{5}\right)\)
Lấy \(B\left(3;0\right)\) là 1 điểm thuộc d
Phương trình đường thẳng \(\Delta'\) qua B và vuông góc \(\Delta\) có dạng:
\(1\left(x-3\right)+1\left(y-0\right)=0\Leftrightarrow x+y-3=0\)
Gọi C là giao điểm \(\Delta\) và \(\Delta'\Rightarrow\) tọa độ C thỏa mãn:
\(\left\{{}\begin{matrix}x+y-3=0\\x-y=0\end{matrix}\right.\) \(\Rightarrow C\left(\dfrac{3}{2};\dfrac{3}{2}\right)\)
B' là ảnh của B qua phép đối xứng trục \(\Delta\Rightarrow B'\in d_1\) và C là trung điểm BB'
\(\Rightarrow\left\{{}\begin{matrix}x_{B'}=2x_C-x_B=0\\y_{B'}=2y_C-y_B=3\end{matrix}\right.\) \(\Rightarrow B'\left(0;3\right)\)
\(\Rightarrow\overrightarrow{AB'}=\left(-\dfrac{3}{5};\dfrac{12}{5}\right)=\dfrac{3}{5}\left(-1;4\right)\)
\(\Rightarrow d_1\) nhận (4;1) là 1 vtpt
Phương trình \(d_1\):
\(4\left(x-0\right)+1\left(y-3\right)=0\Leftrightarrow4x+y-3=0\)
3N
1
QC
2
B
30 tháng 4 2022
pt 2CH3COOH+Mg→(CH3COO)2Mg +H2
n(CH3COO)2Mg =1,42/142=0,1 mol
theo pt nCH3COOH =2n(CH3COO)2Mg =0,2 mol
suy ra CM=0,2 /0,5=0.4 mol/l
theo pt nH2 =n(CH3COO)2Mg =0,1 mol
suy ra VH2 =2,24l
KOH+CH3COOH->CH3COOK+H2O
0,2------0,2
=>VKOH=\(\dfrac{0,2}{0,5}\)=0,4l=400ml
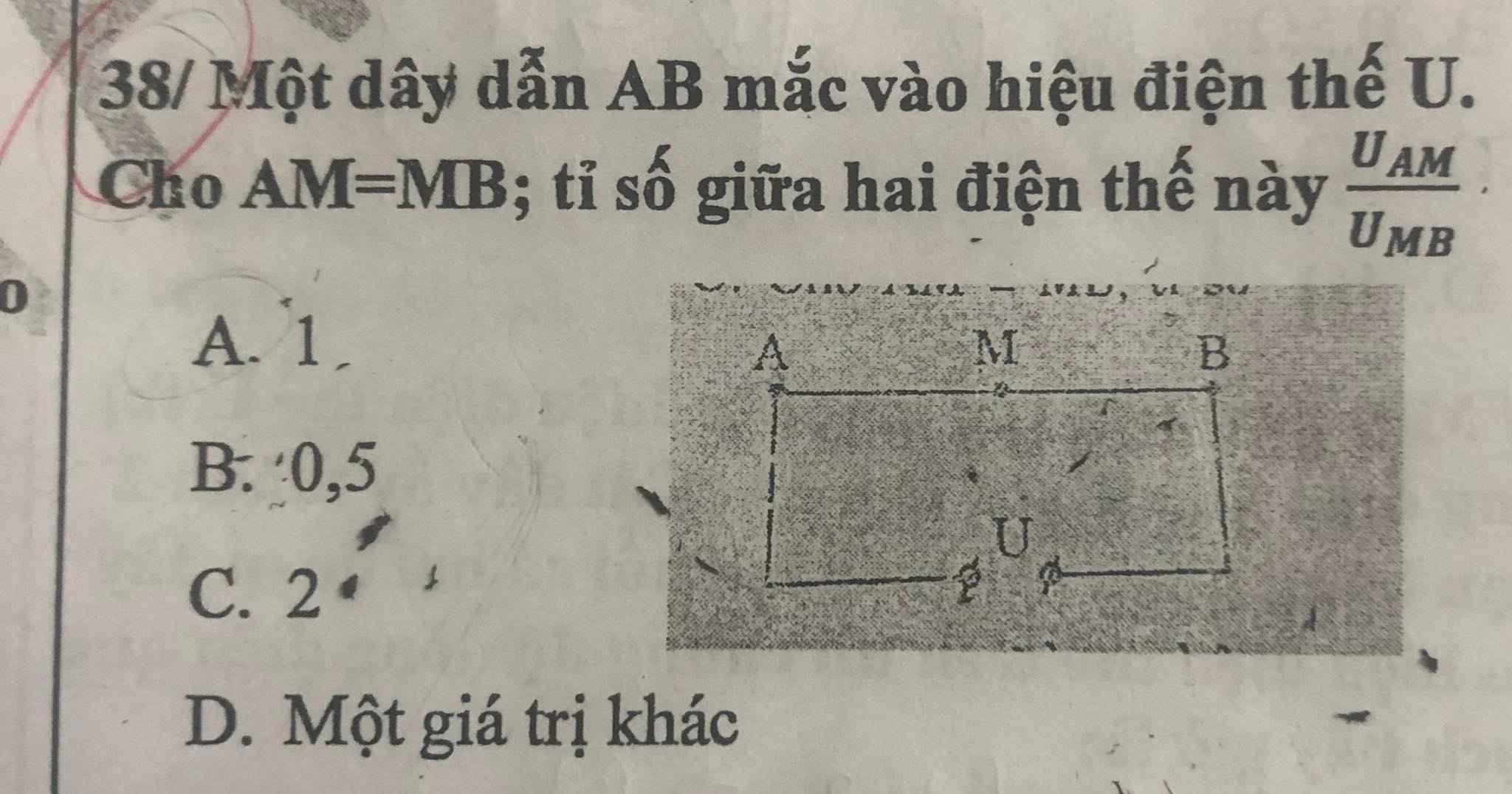
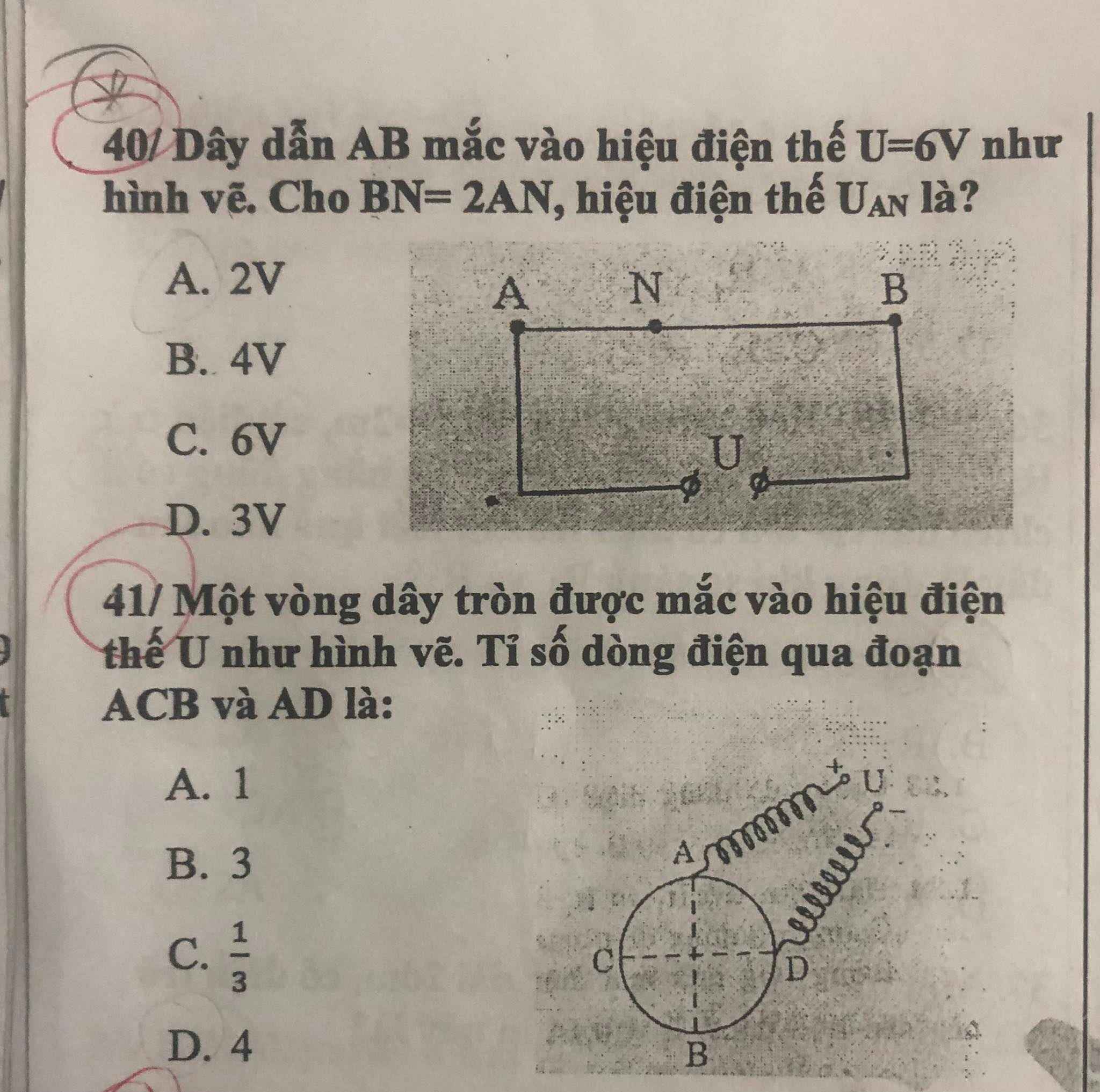
Ai giúp tui với