Cho hình vuông ABCD cạnh a.Tính các tích vô hướng sau: a)AB.AD;AB.BD b)(AB+AD).(BD+BC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 12 2023
a: ABCD là hình vuông
=>AC là phân giác của góc BAD và \(AC^2=AB^2+BC^2\)
AC là phân giác của góc BAD
=>\(\widehat{BAC}=\widehat{DAC}=\dfrac{1}{2}\cdot90^0=45^0\)
\(AC^2=AB^2+BC^2\)
=>\(AC^2=a^2+a^2=2a^2\)
=>\(AC=a\sqrt{2}\)
\(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB};\overrightarrow{AC}\right)\)
\(=a\cdot a\sqrt{2}\cdot cosBAC\)
\(=a^2\cdot\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=a^2\)
b: Vì ABCD là hình vuông
nên AC\(\perp\)BD
=>\(\overrightarrow{AC}\cdot\overrightarrow{BD}=0\)
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
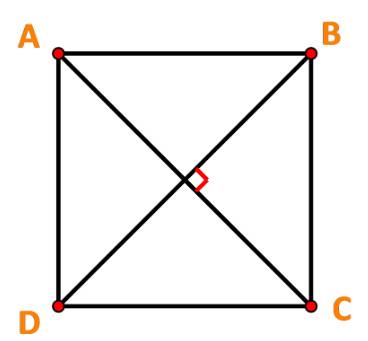
a) Ta có: \(AC = \sqrt {A{B^2} + A{D^2}} = \sqrt {2{a^2}} = a\sqrt 2 \)
\( \Rightarrow \overrightarrow {AB} .\overrightarrow {AC} = a.a\sqrt 2 .\cos \widehat {BAC} = {a^2}\sqrt 2 \cos {45^o} = {a^2}.\)
b) Dễ thấy: \(AC \bot BD \Rightarrow (\overrightarrow {AC} ,\overrightarrow {BD} ) = {90^o}\)
\( \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = AC.BD.\cos {90^o} = AC.BD.0 = 0.\)
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2021
\(\overrightarrow{SA}.\overrightarrow{CD}=\overrightarrow{SA}.\overrightarrow{BA}=\overrightarrow{AS}.\overrightarrow{AB}=a.a.cos60^0=\dfrac{a^2}{2}\)
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
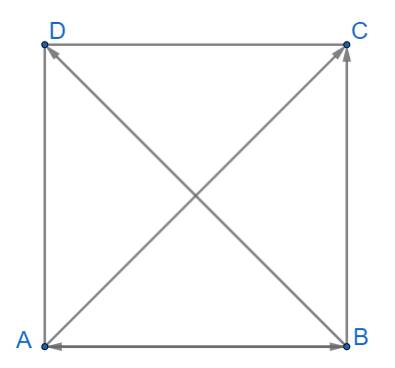
Ta có: \(AC = BD = \sqrt {A{B^2} + B{C^2}} = \sqrt {{a^2} + {a^2}} = a\sqrt 2 \)
+) \(AB \bot AD \Rightarrow \overrightarrow {AB} \bot \overrightarrow {AD} \Rightarrow \overrightarrow {AB} .\overrightarrow {AD} = 0\)
+) \(\overrightarrow {AB} .\overrightarrow {AC} = \left| {\overrightarrow {AB} } \right|.\left| {\overrightarrow {AC} } \right|.\cos \left( {\overrightarrow {AB} ,\overrightarrow {AC} } \right) = a.a\sqrt 2.\cos 45^\circ = a^2\)
+) \(\overrightarrow {AC} .\overrightarrow {CB} = \left| {\overrightarrow {AC} } \right|.\left| {\overrightarrow {CB} } \right|.\cos \left( {\overrightarrow {AC} ,\overrightarrow {CB} } \right) = a\sqrt 2 .a.\cos 135^\circ = - {a^2}\)
+) \(AC \bot BD \Rightarrow \overrightarrow {AC} \bot \overrightarrow {BD} \Rightarrow \overrightarrow {AC} .\overrightarrow {BD} = 0\)
Chú ý
\(\overrightarrow {a} \bot \overrightarrow {b} \Leftrightarrow \overrightarrow {a} .\overrightarrow {b} = 0\)
ND
1
11 tháng 12 2023
ABCD là hình vuông
=>AC\(\perp\)BD
=>\(\overrightarrow{AC}\cdot\overrightarrow{BD}=0\)
21 tháng 12 2022
BM=BC/2=10cm
\(AM=\sqrt{20^2+10^2}=10\sqrt{5}\left(cm\right)\)
Xét ΔABM vuông tại B có sin BAM=BM/AM=10/10căn 5
nên cos BAM=2/căn 5
\(\overrightarrow{AB}\cdot\overrightarrow{AM}=AB\cdot AM\cdot cosBAM=20\cdot10\sqrt{5}\cdot\dfrac{2}{\sqrt{5}}\)
\(=20\cdot10\cdot2=40\cdot10=400\)
AH
Akai Haruma
Giáo viên
28 tháng 1 2021
Lời giải:$ABCD$ là hình vuông nên $AC=\sqrt{2}a$
Ta thấy: $SA^2+SC^2=a^2+a^2=2a^2=AC^2$
$\Rightarrow SAC$ là tam giác vuông tại $S$
$\Rightarrow \overrightarrow{SA}.\overrightarrow{SC}=0$
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
\(\overrightarrow{AC}.\overrightarrow{BD}=\left(\overrightarrow{AD}+\overrightarrow{DC}\right)\left(\overrightarrow{BA}+\overrightarrow{AD}\right)\)
\(=\overrightarrow{AD}.\overrightarrow{BA}+\overrightarrow{AD}^2+\overrightarrow{DC}.\overrightarrow{BA}+\overrightarrow{DC}.\overrightarrow{AD}\)
\(=\overrightarrow{AD}^2-\overrightarrow{AB}.\overrightarrow{DC}=a^2-a.2a=-a^2\)
20 tháng 12 2022
a: AB=BC=CD=DA=6a
\(AC=BD=\sqrt{\left(6a\right)^2+\left(6a\right)^2}=6a\sqrt{2}\)
\(\left|\overrightarrow{AB}-\overrightarrow{AC}\right|=\left|\overrightarrow{CA}+\overrightarrow{AB}\right|=CB=6a\)
\(\left|\overrightarrow{BC}+\overrightarrow{BD}\right|=\sqrt{BC^2+BD^2+2\cdot BC\cdot BD\cdot cos45}\)
\(=\sqrt{36a^2+72a^2+\sqrt{2}\cdot6a\cdot6a\sqrt{2}}\)
\(=6a\sqrt{5}\)
b: \(\overrightarrow{AB}\cdot\overrightarrow{AC}=AB\cdot AC\cdot cos\left(\overrightarrow{AB},\overrightarrow{AC}\right)=6a\cdot6a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}\)
\(=36a^2\)
a: \(\overrightarrow{AB}\cdot\overrightarrow{AD}=0\)
\(\overrightarrow{AB}\cdot\overrightarrow{BD}=\overrightarrow{AB}\left(\overrightarrow{AD}-\overrightarrow{AB}\right)=-AB^2=-a^2\)
b: \(=\overrightarrow{AB}\cdot\overrightarrow{BD}+\overrightarrow{AB}\cdot\overrightarrow{BC}+\overrightarrow{AD}\cdot\overrightarrow{BD}+\overrightarrow{AD}\cdot\overrightarrow{BC}\)
\(=-a^2-\overrightarrow{BA}\cdot\overrightarrow{BC}+\overrightarrow{DA}\cdot\overrightarrow{DB}+AD^2\)
\(=-0+DA\cdot DB\cdot cos45=a\cdot a\sqrt{2}\cdot\dfrac{\sqrt{2}}{2}=a^2\)