Tìm a,b nguyên tố: a2-2b2=1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


P≤√a2+2√aab+2b2+√b2+2√2bc+2c2+√c2+2√2ca+2a2P≤a2+2aab+2b2+b2+22bc+2c2+c2+22ca+2a2
P≤√(a+√2b)2+√(b+√2c)2+√(c+√2a)2P≤(a+2b)2+(b+2c)2+(c+2a)2
P≤

Áp dụng BĐT AM-GM ta có:
\(\frac{2}{3}a^2+\frac{3}{2}b^2\ge2ab\)
\(\frac{b^2}{2}+2c^2\ge2bc\)
\(3c^2+\frac{a^2}{3}\ge2ac\)
\(\Rightarrow2A\le a^2+2b^2+5c^2=22\Rightarrow A\le11\)
\("="\Leftrightarrow a=3;b=2;c=1\)

y ' = a cos x + b sin x = - m
Hàm số đồng biến trên R khi và chỉ khi
y ' ≥ 0 , ∀ x ∈ ℝ ⇔ a sin x + b cos x ≥ m ⇔ m ≤ m i n f x
với f x = a sin x + b cos x
Áp dụng bất đẳng thức Bunhiacopxki ta có:
f x ≤ a 2 + b 2 ⇔ - a 2 + b 2 ≤ f x ≤ a 2 + b 2
Vậy m ≤ - a 2 + b 2
Đáp án C

Chọn đáp án B.
Bằng cách sử dụng điều kiện tồn tại nghiệm của phương trình, chúng ta có: Khi a = 0 thì hàm số chỉ đạt giá trị lớn nhất (khi b < 0) hoặc chỉ đạt giá trị nhỏ nhất (khi b > 0). Còn khi
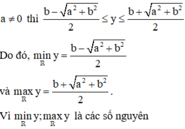
nên tập giá trị của hàm số đã cho chỉ có đúng 6 số nguyên khi và chỉ khi
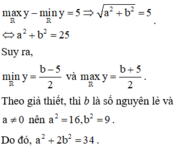

Lời giải:
Không mất tổng quát giả sử $a\leq b\leq c$
Nếu $a,b,c$ đều là số nguyên tố lẻ thì $a^2+b^2+c^2$ là số lẻ. Mà $5070$ chẵn nên vô lý.
Do đó trong 3 số $a,b,c$ tồn tại ít nhất 1 số chẵn.
Số nguyên tố chẵn luôn là số bé nhất (2) nên $a=2$
Khi đó: $b^2+c^2=5070-a^2=5066\geq 2b^2$
$\Rightarrow b^2\leq 2533$
$\Rightarrow b< 51$
$\Rightarrow b\in \left\{2; 3; 5; 7; 11; 13; 17; 19; 23; 29; 31; 37; 41; 43; 47\right\}$
Thử các TH này ta thấy $(b,c)=(5,71), (29,65)$
Vậy $(a,b,c)=(2,5,71), (2,29,65)$ và các hoán vị.
vì 5070 là số chẵn ⇒ một trong 3 số a,b,c chẵn hoặc cả 3 số a,b,c chẵn
+) cả 3 số a,b,c chẵn
=> a=2, b=2, c=2 ( vì a,b,c là các số nguyên tố )
khi đó: a2+b2+c2= 12(loại)
=> một trong 3 số a,b,c chẵn
vì giá trị các số bằng nhau, giả sử a chẵn => a=2
khi đó: a2+b2+c2= 4+b2+c2
=> b2+c2= 5066
vì số chính phương có tận cùng là 0, 1, 4, 5, 6, 9 mà b2 và c2 là số chính phương có tận cùng là 0, 1, 4, 5, 6, 9
=> b2 và c2 có tận cùng là 0, 1, 4, 5, 6, 9
Mà b và c lẻ
=> b2 và c2 có tận cùng là 1, 5, 9
mà 5066 có tận cùng là 6
=> b2 và c2 có tận cùng là 1, 5
=> b và c có tận cùng là 1, 5
giả sử b có tận cùng là 5=> b=5
khi đó: 25+ c2 = 5066
c2 = 5041=712
=> c = 71
vậy, a=2, b=5, c=71 và các hoán vị của nó
Ta thấy 1 là số lẻ nên suy ra a2 phải là số lẻ hay a là số lẻ
\(\Rightarrow a=2k+1\)
\(\Rightarrow a^2-2b^2=1\)
\(\Leftrightarrow\left(2k+1\right)^2-2b^2=1\)
\(\Leftrightarrow4k^2-4k+1-2b^2=1\)
\(\Leftrightarrow2\left(k^2-k\right)=b^2\)
\(\Rightarrow b^2⋮2\)
\(\Rightarrow b⋮2\)
Mà b là số nguyên tố nên b = 2
\(\Rightarrow a=3\)
Sai to rồi: \(\left(a+b\right)^2=\left(a^2+2ab+b^2\right)\\ \) Phải học lại HĐT thôi/%%