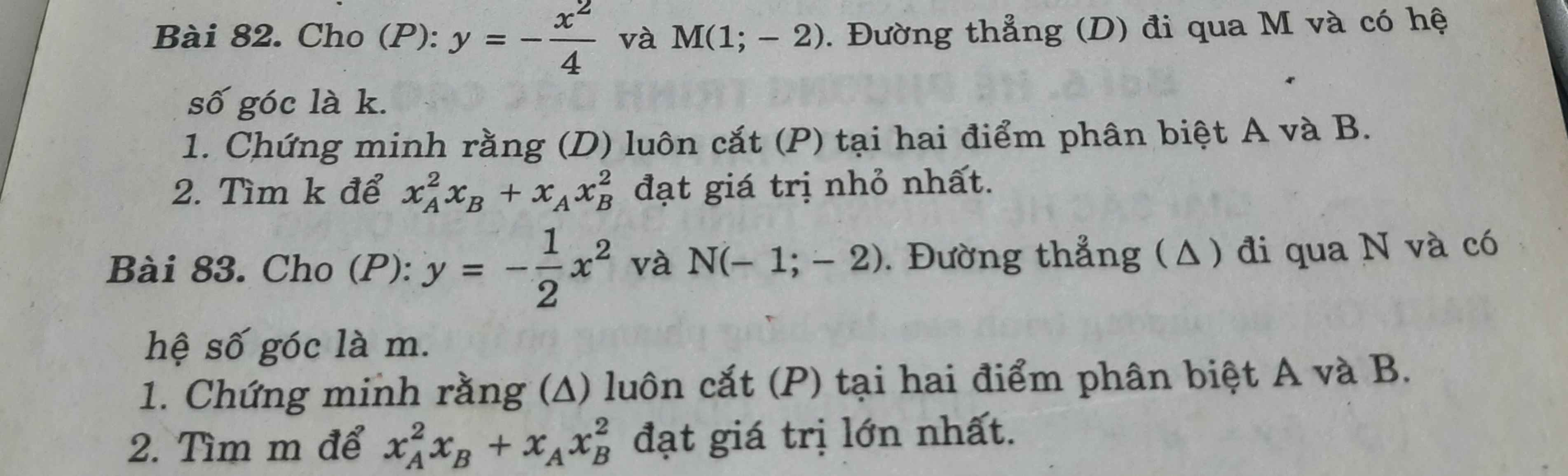Giúp mình câu 83
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có : \(\left\{{}\begin{matrix}\dfrac{1}{14}< \dfrac{1}{10}\\\dfrac{1}{23}< \dfrac{1}{10}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{14}+\dfrac{1}{23}< \dfrac{1}{10}+\dfrac{1}{10}=\dfrac{1}{5}\)
Lại có : \(\left\{{}\begin{matrix}\dfrac{1}{62}< \dfrac{1}{60}\\\dfrac{1}{83}< \dfrac{1}{60}\\\dfrac{1}{117}< \dfrac{1}{60}\end{matrix}\right.\)
\(\Rightarrow\dfrac{1}{62}+\dfrac{1}{83}+\dfrac{1}{117}< \dfrac{1}{60}+\dfrac{1}{60}+\dfrac{1}{60}=\dfrac{1}{20}\)
\(\Rightarrow\dfrac{1}{5}+\dfrac{1}{14}+\dfrac{1}{23}+\dfrac{1}{62}+\dfrac{1}{83}+\dfrac{1}{117}< \dfrac{1}{5}+\dfrac{1}{5}+\dfrac{1}{20}=\dfrac{9}{20}< \dfrac{10}{20}=\dfrac{1}{2}\)



Phương trình \(\Delta\) có dạng:
\(y=m\left(x+1\right)-2\Leftrightarrow y=mx+m-2\)
Phương trình hoành độ giao điểm (P) và \(\Delta\):
\(-\dfrac{1}{2}x^2=mx+m-2\Leftrightarrow x^2+2mx+2m-4=0\) (1)
\(\Delta'=m^2-2m+4=\left(m-1\right)^2+3>0\) ; \(\forall m\)
\(\Rightarrow\) (1) luôn có 2 nghiệm pb với mọi m hay (P) luôn cắt \(\Delta\) tại 2 điểm pb
b.
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_A+x_B=-2m\\x_Ax_B=2m-4\end{matrix}\right.\)
Đặt \(A=x_A^2x_B+x_Ax_B^2=x_Ax_B\left(x_A+x_B\right)\)
\(A=-2m\left(2m-4\right)=-4m^2+8m=-4\left(m-1\right)^2+4\le4\)
\(A_{max}=4\) khi \(m=1\)

98 - 217 + 102 - 83 - 2022
= (98 + 102) - (217 + 83) - 2022
= 200 - 300 - 2022
= - 100 - 2022
= - 2122

83 - 5 ( x + 4 ) = 28
5 ( x + 4 ) = 83 - 28
5 ( x + 4 ) = 55
x + 4 = 55 : 5
x + 4 = 11
x = 11 - 4
x = 7