Câu 16. (1,0 điểm): Cho biết công thức tính diện tích hình tròn bán kính ${R}$ là ${S}=\pi {R}^2$. Sử dụng MTCT, hãy tính độ dài bán kính (tính theo đơn vị xen ti mét - với độ chính xác $d=0,05$) của hình tròn có diện tích bằng $100$ cm$^2$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Độ dài cạnh của một mảnh đất hình vuông là:
\(\sqrt {12\,\,996} = 114\)(m)
b) Bán kính của hình tròn là:
\(S = \pi {R^2} \Rightarrow R^2 = \frac{S}{\pi } \Rightarrow R = \sqrt {\frac{S}{\pi }} = \sqrt {\frac{{100}}{\pi }} \approx 5,64\)(cm)

Diện tích hình tròn là: \(S = 3,{142.10^2} = 314,2 (\,c{m^2})\)

Chu vi của hình tròn đó là:
C = 2πR = 2.3,142.1,25 = 7,855 (m)
Đáp số: 7,855 m


a = 200
=> Chiều rộng khu đất hcn là:
200 x 3/4 = 150 (đơn vị)
Diện tích khu đất hcn là:
200 x 150 = 30000 (đơn vị)
Bán kính cái giếng hình tròn là:
150 x 1/4 = 37,5 (đơn vị)
Diện tích cái giếng hình tròn là:
37,5 x 37,5 x 3,14 = 4415,625 (đơn vị)
Diện tích phần còn lại là:
30000 - 4415,625 = 25584,375 (đơn vị)
Đ/s:..

Lời giải:
Diện tích xung quanh hình nón:
$\pi (r+R).l=\pi (6+3).4=36\pi$ (cm vuông)
Diện tích toàn phần:
$36\pi+\pi r^2+\pi R^2=36\pi +\pi.3^2+\pi. 6^2=81\pi$ (cm vuông)
Thể tích:
Chiều cao hình nón: $\sqrt{4^2-(6-3)^2}=\sqrt{7}$ (cm)
$\frac{1}{3}\pi (r^2+R^2+r.R)h=\frac{1}{3}\pi (3^2+6^2+3.6).\sqrt{7}=21\sqrt{7}\pi$ (cm khối)
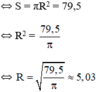

Thay �=100S=100 vào �=��2S=πR2 ta được ��2=100πR2=100.
Suy ra �=100�R=π100.
Sử dụng MTCT tính được �=5,641895835...R=5,641895835...
Cần làm tròn đến hàng phần chục để có độ chính xác �=0,05d=0,05.
Kết quả là �≈5,6R≈5,6.