Tìm điểm I sao cho tổng khoảng cách từ I đén A, B, C, D có độ dài ngắn nhất. A B C D
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
16 tháng 8 2021
Gọi D là điểm đối xứng A qua d \(\Rightarrow\) d là trung trực AD \(\Rightarrow CA=CD\)
Nối BD cắt d tại M
Do BD là đường thẳng và BCD là đường gấp khúc nên ta luôn có:
\(BC+CD\ge BM+MD\)
\(\Leftrightarrow CB+CA\ge BD\)
Dấu "=" xảy ra khi và chỉ khi C trùng M
\(\Rightarrow\) Độ dài CA+CB ngắn nhất khi C là giao điểm của BD và d, trong đó D là điểm đối xứng với A qua d
29 tháng 6 2017
Xét hai trường hợp :
- Trường hợp A và B nằm cùng phía đối với đường thẳng d (h.bs.6a). Ta tính được :
\(CH=\dfrac{20+6}{2}=13\left(cm\right)\)
- Trường hợp A và B nằm khác phía đối với đường thẳng d (h.bs.6b). Ta tính được :
\(CH=CK-HK=10-3=7\left(cm\right)\)
CM
16 tháng 2 2018
Mặt phẳng ( ABC ) có VTPT
n → = C A → , C B → = [ ( 1 ; 1 ; - 3 ) , ( 0 ; 3 ; - 3 ) ] = 3 2 ; 1 ; 1
Suy ra PT ( ABC ) : 2x + y + z -1 = 0
Dễ thấy I ∈ A B C nên khoảng cách từ D đến mặt phẳng (ABC) có giá trị lớn nhất bằng bán kính và bằng 3
Đáp án cần chọn là D
CM
25 tháng 1 2019
Đáp án B.
Ta thấy D ∈ ( A B C ) : 2 x + 3 y + z = 0
Ta có: d A , d ≤ A D d B , d ≤ B D d C , d ≤ C D ⇒ d A , d + d B , d + d C , d ≤ A D + B D + C D
Dấu “=” xảy ra khi d ⊥ A B C tại điểm D ⇒ d : x = 1 + 2 t y = 1 + 3 t z = z + t ⇒ N 5 ; 7 ; 3 ∈ d
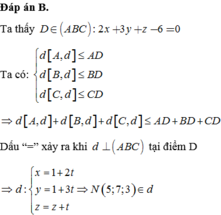
S = IA + IC + IB + ID
IA + IC ngắn nhất khi I thuộc AC
IB + ID ngắn nhất khi I thuộc BD
Vậy IA + IC + IB + ID ngắn nhất khi I vừa thuộc AC, vừa thuộc BD
=> I là giao điểm AC và BD