tìm x,y biết:
K
Khách
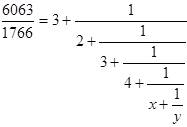
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 4 2020
*) Ta có a(b-2)=3
Vì a,b là số nguyên => a,b-2 thuộc Ư(3)={-3;-1;1;3}
Vì a>0 => a={1;3}
Ta có bảng
| a | 1 | 3 |
| b-2 | 3 | 1 |
| b | 5 | 3 |
b) (x-2)(y+1)=23
=> x-2;y+1 thuộc Ư(23)={-23;-1;1;23}
Ta có bảng
| x-2 | -23 | -1 | 1 | 23 |
| x | -21 | 1 | 3 | 25 |
| y+1 | -1 | -23 | 23 | 1 |
| y | -2 | -24 | 22 | 0 |
6 tháng 4 2020
1. \(a\left(b-2\right)=3\)
Ta có : \(3=\orbr{\begin{cases}3\cdot1\\-3\cdot\left(-1\right)\end{cases}}\)
* a = 3 ; b - 2 = 1 => b = 3
* a = 1 ; b - 2 = 3 => b = 5
* a = -1 ; b - 2 = -3 => b = -1
* a = -3 ; b - 2 = -1 => b = 1
2. \(\left(x-2\right)\left(y+1\right)=23\)
Ta có : \(23=\orbr{\begin{cases}23\cdot1\\-23\cdot\left(-1\right)\end{cases}}\)
* x - 2 = 23 ; y + 1 = 1 => x = 25 ; y = 0
* x - 2 = 1 ; y + 1 = 23 => x = 3 ; 22
* x - 2 = -23 ; y + 1 = -1 => x = -21 ; y = -2
* x - 2 = -1 ; y + 1 = -23 => x = 1 ; y = -24
LH
0
NT
1
DD
Đoàn Đức Hà
Giáo viên
17 tháng 10 2021
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x-1}{2}=\frac{y-2}{3}=\frac{z-3}{4}=\frac{x-1-2\left(y-2\right)+3\left(z-3\right)}{2-2.3+3.4}=\frac{x-2y+3z-6}{8}=1\)
\(\Leftrightarrow\hept{\begin{cases}x-1=2\\y-2=3\\z-3=4\end{cases}}\Leftrightarrow\hept{\begin{cases}x=3\\y=5\\z=7\end{cases}}\)
NT
1
NK
0
TM
20 tháng 11 2016
\(x+y=3\left(x-y\right)\Leftrightarrow x+y=3x-3y\Leftrightarrow4y=2x\Leftrightarrow x:y=2\Leftrightarrow x=2y\)
\(x:y=2\Leftrightarrow x+y=2\Leftrightarrow2y+y=2\Leftrightarrow3y=2\Leftrightarrow y=\frac{2}{3}\)
\(x+y=2\Leftrightarrow x+\frac{2}{3}=2\Leftrightarrow x=2-\frac{2}{3}=\frac{4}{3}\)
Vậy \(x=\frac{4}{3}\) và \(y=\frac{2}{3}\)
\(\dfrac{6063}{1766}=3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}}\)
\(3\dfrac{765}{1766}=3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}}\)
\(\dfrac{765}{1766}=\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}}\)
\(\dfrac{1766}{765}=2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}\)
\(2\dfrac{236}{765}=2+\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}\)
\(\dfrac{236}{765}=\dfrac{1}{3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}}\)
\(\dfrac{765}{236}=3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}\)
\(3\dfrac{57}{236}=3+\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}\)
\(\dfrac{57}{236}=\dfrac{1}{4+\dfrac{1}{x+\dfrac{1}{y}}}\)
\(\dfrac{236}{57}=4+\dfrac{1}{x+\dfrac{1}{y}}\)
\(4\dfrac{8}{57}=4+\dfrac{1}{x+\dfrac{1}{y}}\)
\(\dfrac{8}{57}=\dfrac{1}{x+\dfrac{1}{y}}\)
\(\dfrac{57}{8}=x+\dfrac{1}{y}\)
\(\dfrac{57}{8}=\dfrac{xy+1}{y}\)
\(\left(\dfrac{xy+1}{y}\right)làphânsốtốigiản\)
=> y = 8
=> xy+1 = 57
=> 8x + 1 =57
=> 8x = 56
=> x = 56/8=7
Vậy x = 7 và y = 8