Cho tam giac ABC cos 3 duong trung tuyen AD=12, BE=9, CF=15. Tinh BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a/ Tính độ dài các cạnh AM, BN, CE?
b/ Tính diện tích Δ ABC
Dưới đây là ý a tớ đã làm ( bạn tự vẽ hình nhé )
a/ Xét ΔABC có góc A=90°
mà AM là trung tuyến của ΔABC
=> AM=BC/2=13/2=6,5(cm)
Xét ΔABC có góc A = 90°
Áp dụng đ/lí Py-ta-go có:
BC^2=AE^2+AC^2
=> AC^2=BC^2-AE^2
AC^2=13^2-5^2=144 => AC=√144=12(cm)
Xét ΔABN có góc A=90°
mà BN là trung tuyến của Δ ABC
=> BN=AC/2=12/2=6(cm)
BN^2=AB^2+AN^2
BN^2=5^2+6^2
BN^2=61 => BN= √61(cm)
Xét ΔACE có góc A=90 °
AC=12cm, AE=AB/2=2,5(cm) [CE là trung tuyến]
Áp dụng đ/lí Py-ta-go có:
CE^2=AC^2+AE^2
CE^2=12^2+2,5^2
CE^2= 144 + 6,25
=> CE^2=150,25 => CE=√ 150,25 (cm)

A,
xét \(\Delta ABD\)và \(\Delta ACD\)
CÓ \(\hept{\begin{cases}AB=AC\\chungAD\\BD=DC\end{cases}}\)
SUY RA \(\Delta ABD\)=\(\Delta ACD\) (C.C.C) (1)
=> \(\widehat{BDA}\)=\(\widehat{CDA}\)
MÀ \(\widehat{BDA}\)+\(\widehat{CDA}\)=180
=> \(\widehat{BDA}\)=\(\widehat{CDA}\)=90
B, (1) => BC=DC=1/2 BC=8
ÁP DỤNG ĐỊNH LÍ PITAGO TA CÓ
\(AB^2=AD^2+BD^2\)
=> AD^2=36
=>AD=6

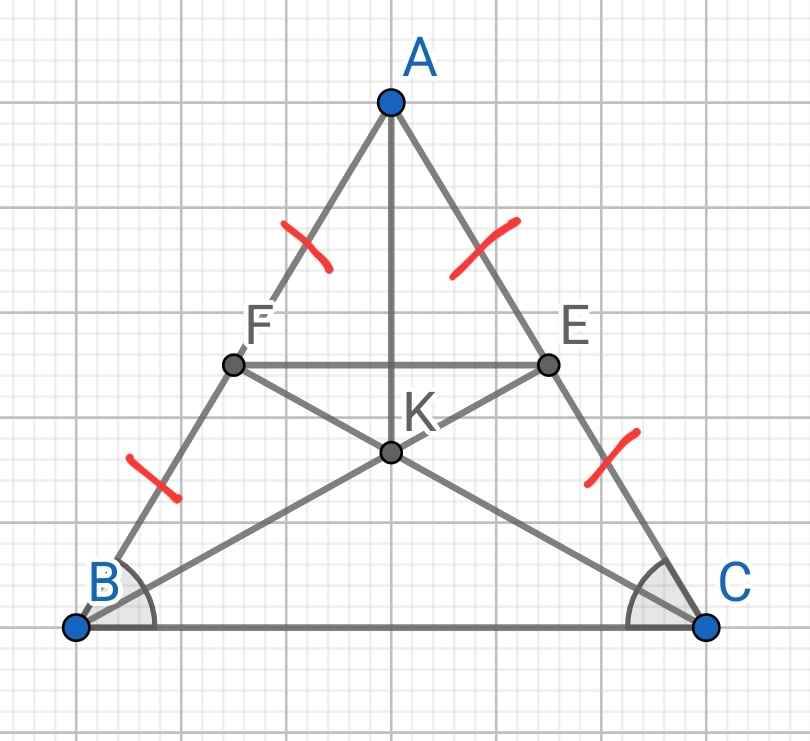 1.
1.
a) Do ∆ABC cân tại A (gt)
⇒ AB = AC và ∠ABC = ∠ACB (1)
Do BE là đường trung tuyến của ∆ABC (gt)
⇒ E là trung điểm của AC
⇒ AE = CE = AC/2 (2)
Do CF là đường trung tuyến của ∆ABC (gt)
⇒ F là trung điểm của AB
⇒ AF = BF = AB/2 (3)
Từ (1), (2) và (3) ⇒ BF = CE
Do ∠ABC = ∠ACB (cmt)
⇒ ∠FBC = ∠ECB
Xét ∆BFC và ∆CEB có:
BF = CE (cmt)
∠FBC = ∠ECB (cmt)
BC chung
⇒ ∆BFC = ∆CEB (c-g-c)
⇒ CF = BE (hai cạnh tương ứng)
Hay BE = CF
b) Do ∆BFC = ∆CEB (cmt)
⇒ ∠BCF = ∠CBE (hai góc tương ứng)
⇒ ∠BCK = ∠CBK
∆BKC có:
∠BCK = ∠CBK (cmt)
⇒ ∆BKC cân tại K
c) Do ∆BKC cân tại K (cmt)
⇒ BK = CK
Do ∠ABC = ∠ACB (cmt)
⇒ ∠ABK = ∠ABC - ∠CBK = ∠ACB - ∠BCK = ∠ACK
⇒ ∠FBK = ∠ECK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
∠FBK = ∠CEK (cmt)
BF = CE (cmt)
⇒ ∆BFK = ∆CEK (c-g-c)
⇒ FK = EK (hai cạnh tương ứng)
d) Sửa đề: Chứng minh ∆BFK = ∆CEK
Xét ∆BFK và ∆CEK có:
BK = CK (cmt)
BF = CE (cmt)
FK = EK (cmt)
⇒ ∆BFK = ∆CEK (c-c-c)
2.
a) Từ (1), (2) và (3) ⇒ AF = AE
∆AEF có:
AE = AF (cmt)
⇒ ∆AEF cân tại A
b) Do ∆ABC cân tại A (gt)
⇒ ∠ABC = ∠ACB = (180⁰ - ∠BAC) : 2 (4)
Do ∆AEF cân tại A (cmt)
⇒ ∠AFE = ∠AEF = (180⁰ - ∠FAE) : 2
⇒ ∠AFE = ∠AEF = (180⁰ - ∠BAC) : 2 (5)
Từ (4) và (5) ⇒ ∠ABC = ∠AFE
Mà ∠ABC và ∠AFE là hai góc đồng vị
⇒ EF // BC
c) Xét ∆AFK và ∆AEK có:
AF = AE (cmt)
AK chung
FK = EK (cmt)
⇒ ∆AFK = ∆AEK (c-c-c)