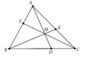
cho tam giác ABC và M nằm trong tam giác. Kéo dài AM, BM, CM cắt các cạnh đối diện tại A1, B1, C1. CMR: MA1+MB1+MC1< Max { AB, BC, CA }
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\sqrt{\frac{AM}{A_1M}}+\sqrt{\frac{BM}{B_1M}}+\sqrt{\frac{CM}{C_1M}}=\sqrt{\frac{S_2+S_3}{S_1}}+\sqrt{\frac{S_1+S_3}{S_2}}+\sqrt{\frac{S_1+S_2}{S_3}}\)
\(\ge\sqrt{\frac{\left(\sqrt{S_2}+\sqrt{S_3}\right)^2}{2S_1}}+\sqrt{\frac{\left(\sqrt{S_1}+\sqrt{S_3}\right)^2}{2S_2}}+\sqrt{\frac{\left(\sqrt{S_1}+\sqrt{S_2}\right)^2}{2S_3}}\)
\(=\frac{1}{\sqrt{2}}\left(\frac{\sqrt{S_2}+\sqrt{S_3}}{\sqrt{S_1}}+\frac{\sqrt{S_1}+\sqrt{S_3}}{\sqrt{S_2}}+\frac{\sqrt{S_1}+\sqrt{S_2}}{\sqrt{S_3}}\right)\frac{1}{2}\cdot6=3\sqrt{2}\)
Dấu "=" xảy ra khi S1 =S2=S3 <=> M là trọng tâm \(\Delta ABC\)

cho tam giác ABC. Các điểm D, E, F lần lượt thuộc AB, AC, BC. chứng minh rằng: a) diện tích ADE trên diện tích ABC bằng AD*AE trên AB*AC . b) Trong 3 tam giác ADE, BDF, CEF tồn tại 1 tam giác có diện tích không vượt quá 1/4 diện tích ABC. Khi nào cả 3 tam giác đó cùng có diện tích = 1/4 diện tích ABC