Cho tam giác ABC có AB=AC. trên tia đối của tia BA,CA lần lượt lấy hai điểm M,N sao cho BM=CN. CMR BC//MN
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi E là giao điểm các đường trung trực của MN và BC.
Theo tính chất đường trung trực ta có \(\left\{{}\begin{matrix}EM=EN\\EB=EC\end{matrix}\right.\).
Lại có BM = CN (gt) nên \(\Delta EMB=\Delta ENC(c.c.c)\).
Suy ra \(\widehat{EMB}=\widehat{ENC}\) nên \(\widehat{EMA}=\widehat{END}\).
Lại có BM = CN và AB = CD nên AM = ND.
Xét \(\Delta EMA\) và \(\Delta END\) có: \(\left\{{}\begin{matrix}AM=ND\\\widehat{EMA}=\widehat{END}\\EM=EN\end{matrix}\right.\)
\(\Rightarrow\Delta EMA=\Delta END\left(c.g.c\right)\Rightarrow EM=EN\).
Suy ra E thuộc đường trung trực của MN.
Vậy đường trung trực của ba đoạn AD, MN, BC đồng quy.

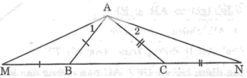
Trong ΔABC, ta có AC > AB
Suy ra: ∠(ABC) > ∠(ACB) (đối diện với cạnh lớn hơn là góc lớn hơn) (1)
Ta có: AB = BM (gt) ⇒ ΔABM cân tại B
Suy ra: ∠(AMB) = ∠A1(tính chất tam giác cân)
Trong ΔABM, ta có ∠(ABC) là góc ngoài tại đỉnh B
Suy ra: ∠(ABC) = ∠(AMB) + ∠A1 hay : ∠(ABC) = 2.∠(AMB)
Suy ra: ∠(AMB) = 1/2 ∠(ABC) (2)
Lại có: AC = CN (gt) ⇒ ΔACN cân tại C
Suy ra: ∠(ANC) = ∠A2(tính chất tam giác cân)
Trong ΔACN, ta có ∠(ACB) là góc ngoài tại đỉnh C
Suy ra: ∠(ACB) = ∠(ANC) + ∠A2 hay ∠(ACB) = 2∠(ANC)
Suy ra: ∠(ANC) = 1/2 ∠(ACB) (3)
Từ (1), (2) và (3) suy ra: ∠(AMB) > ∠(ANC) .

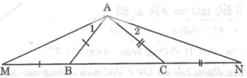
Trong ΔAMN, ta có: ∠(AMB) > ∠(ANC)
Suy ra: AN > AM (đối diện với góc lớn hơn là cạnh lớn hơn).

giải :
Xét tam giác ABC cân tại A có:
góc ABC = góc ACB (t/c)
mà góc MIB = góc ACB ( 2 góc đồng vị do MI//AC)
=> góc ABC = góc MIB
hay góc MBI = góc MIB => tam giác MIB cân tại M ( dấu hiệu nhận biết)
=> MB=MI ( t/c)
Mà MB= CN (gt)
=> MI=CN
Xét tứ giác MINC có
MI// CN (gt)
MI = CN (cmt)
=> tứ giác MINC là hình bình hành ( dấu hiệu nhận biết)
Xét hình bình hành MINC có
MN giao với IC tại O (gt)
=> O là trung điểm của MN(t/c)
=> OM= ON
Vậy OM=ON
