Qua điểm C ở ngoài (O;R) kẻ 2 tiếp tuyến ca và bc với đường tròn(ab là tiếp điểm) kẻ ae vuông góc bc (e thuộc bc) kẻ bt vuông góc ac (f thuộc ac) gọi giao điểm ae và bt tại h
a) chứng minh Oà vuông góc bc
b) so sánh cn và cb
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Xét tam giác MAD và tam giác MCA có
^M _ chung
^MDA = ^MAC ( cùng chắn cung CA )
Vậy tam giác MAD ~ tam giác MCA (g.g)
\(\dfrac{MA}{MC}=\dfrac{MD}{MA}\Rightarrow MA^2=MD.MC\)(1)
b, Vì MA là tiếp tuyến đường tròn (O) với A tiếp điểm
Lại có OA = OB = R ; MA = MB ( tc tiếp tuyến cắt nhau )
=> OM là trung trực đoạn BA
Xét tam giác MAO đường cao AH ta có
\(MA^2=MO.MH\)(2)
Từ (1) ; (2) suy ra \(MO.MH=MD.MC\)

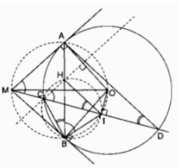

A, B, I nhìn MO cố định dưới một góc bằng 90° nên A, B, I nằm trên đường tròn bán kính MO.
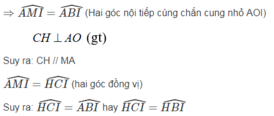
B và C cùng nằm trên một nửa mặt phẳng bờ chứa đường HI tạo với HI một góc bằng nhau nên tứ giác BCHI nội tiếp.


Từ một điểm A ở ngoài đường tròn (O) vẽ 2 tiếp tuyến AB,AC với đường tròn (B,C là 2 tiếp điểm). Qua O vẽ đường thẳng vuông góc với OC; qua A vẽ đường thẳng này vuông góc với AC.Hai đường thẳng này cắt nhau tại D.
a) Chứng minh OA qua trung điểm H của BC và 5 điểm A,D,B,O,C cùng nằm trên một đường tròn.
b) Gọi M, N lần lượt là trung điểm của OD và AH.Chứng minh MN vuông góc CN
c) OD cắt AB tại E.Chứng minh OE.OD + AE.AB = OA^2
a: Xét (O) có
AB,AC là tiếp tuyến
=>AB=AC
mà OB=OC
nên OA là trung trực của BC
=>OA đi qua trung điểm của BC
Xét tứ giác OCAD có
góc OCA=góc COD=góc DAC=90 độ
=>OCAD là hình chữ nhật
=>O,C,A,D nằm trên đường tròn đường kính OA
góc OBA=90 độ
=>B nằm trên đường tròn đường kính OA
=>O,C,A,D,B cùng nằm trên 1 đường tròn

Tóm tắt thôi nhé
a) Các cạnh // => Hình bình hành
T/g OBE = t/g OCD (^B=^C=90*, OB=OC, ^BOE=^COD vì cùng phụ với EOD) => OE = OD (2 cạnh kề) => Hình thoi
b) Nối OO' => 2 tam giác cân cùng góc đáy => so le trong => //
c) 1] OO' là đường trung trực của AB => đường trung bình
2] CB//OO'
Cm tương tự 1] để được BD//OO' => Ơ-clit => thẳng hàng