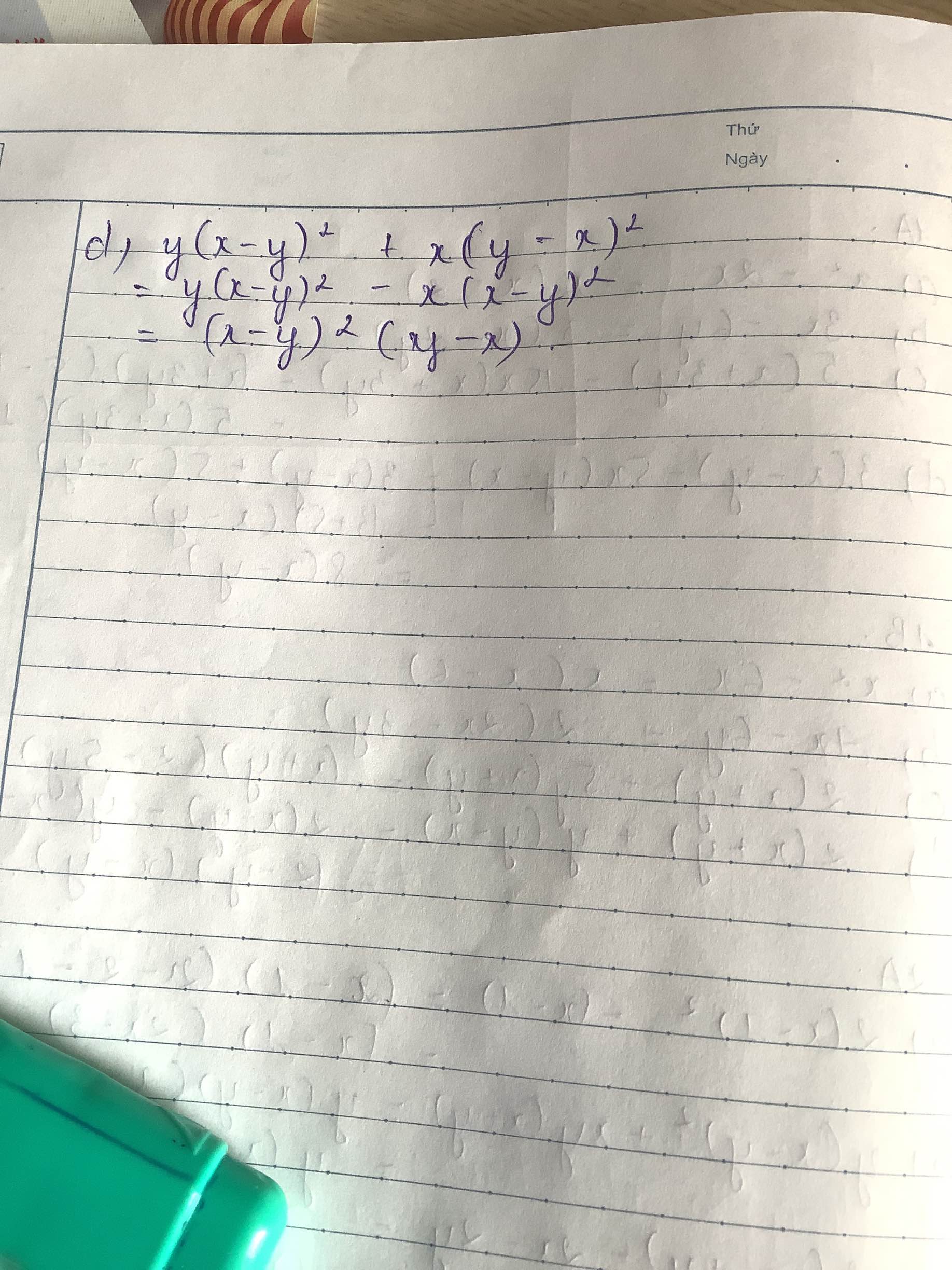Mn giúp mình với🙏


Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Em có thể lên mạng, wikipedia tra cứu những thông tin về lịch sử hình thành, cấu trúc núi, hình dạng núi nhìn từ xa, những lễ hội tại đó, ...và tự viết thành 1 bài văn. Sau đó em đăng lên đây anh sửa cho nhé!
Tham khảo
Núi Bà Đen – một quần thể di tích lịch sử - văn hóa và danh thắng, từ lâu vốn là biểu tượng về đất và người của quê hương Tây Ninh. Núi trải rộng trên diện tích 24km2, gồm 3 ngọn núi tạo thành: núi Heo, núi Phụng và núi Bà Đen. Núi Bà Đen cao 986m, là ngọn núi nhô lên giữa đồng bằng và cao nhất Nam Cách đây 300 năm, nơi đây còn là vùng rừng già hoang vu, hiểm trở. Cùng với bước chân của cộng đồng người Việt đến vùng đất Tân Ninh xưa khai mở đất đai, sinh cơ lập nghiệp, thì các tăng ni, phật tử cũng đồng thời đến đây lập những am, miếu xây dựng chùa chiền để thờ Phật. Trong đó, hệ thống am, điện, chùa, hang động ở núi Bà Đen đã từ lâu thu hút đông đảo khách thập phương đến viếng lễ hàng năm.
Núi Bà Đen được sách Đại Nam nhất thống chí ghi: “Linh Sơn cách Tân Ninh 20 dặm về phía tây bắc, hình núi cao chót vót là trấn sơn của tỉnh, phía tây giáp địa giới Cao Miên, lưng núi có chùa đá ít người đi đến”.
Truyền thuyết về Bà Đen, Linh Sơn thánh mẫu, với hệ thống chùa, điện, am động… cùng với nhiều sự tích trong các cuộc kháng chiến chống ngoại xâm đã tô đậm các sự kiện lịch sử trên núi Bà Đen.
Với cảnh quan hùng vĩ của núi đã tạo nên khu di tích lịch sử - văn hóa nổi tiếng ở Nam bộ và cả nước. Hiện nay, hàng năm thu hút hơn nữa triệu lượt người khắp nơi trong nước đến chiêm bái và du ngoạn.
Từ năm 1983, con đường từ thị xã Tây Ninh đến núi dài 11km đã được trải nhựa với hệ thống điện lưới quốc gia đã nối mạng đến núi. Các cơ sở hạ tầng tại khu di tích được xây dựng hoàn chỉnh. Một bia đài tưởng niệm và vườn hoa được xây dựng. Con đường từ chân núi đến chùa Bà, chùa Hang được nâng cấp mở rộng, cùng với hệ thống nhà trạm dừng chân cho khách hành hương. Đặc biệt, hệ thống cáp treo đưa khách từ chân núi lên chùa Bà được xây dựng và đưa vào sử dụng đầu năm 1998. Với nhiều dịch vụ khác nhằm tạo điều kiện thuận lợi cho khách đi tới các di tích, hang động trong toàn bộ quần thể di tích.
Khu vực Suối Vàng nằm ở phía Tây núi Phụng với hồ Chầm, sân quần ngựa và đền thờ Quan lớn Trà Vong, cùng với đường ô tô được mở rộng lên lưng chừng núi Phụng, xưa có những ngôi chùa cổ, tạo cho vùng Suối Vàng Ma thiên lãnh thành trung tâm văn hóa độc đáo.
Phía bắc núi Heo là căn cứ địa của liên đội 7 anh hùng trong thời chống Mỹ. Với những hang động lớn, nhiều bãi đá trắng, trải rộng trên sườn núi. Phía đông núi Bà có suối tràn, nước chảy quanh năm bởi một tản đá khổng lồ chặn ngang lưng chừng núi. Phía dưới tản đá khổng lồ này có hệ thống hang động. Nơi đây từng là căn cứ của Huyện ủy huyện Dương Minh Châu, Huyện ủy Tòa Thánh (nay là Hòa Thành) trong thời chống Mỹ. Ở lưng chừng xung quanh núi là cả hệ thống hang động từng được các tăng ni, phật tử cải biến thành am, động, miếu, thờ. Những hang tiêu biểu như: hang Gió, chùa Hang, động Thanh Long, động Ông Hổ, động Ông Tà, động Ba Cô và động Thiên Thai… từng là căn cứ địa vững chắc của quân dân Tây Ninh trong các cuộc kháng chiến giải phóng dân tộc.
Núi Bà Đen có nhiều loại gỗ quý hiếm cùng các loại động thực vật phong phú như ốc, dơi, thằn lằn, cheo, mễnh, nai và các loại cây rau, quả có giá trị. Song do chiến tranh tàn phá và sự khai thác bừa bãi của con người nên thảm thực, động vật ở núi Bà Đen hiện còn không đáng kể.
Khi nói đến núi Bà Đen người ta nghỉ ngay đến Điện Bà hay Linh Sơn Tiên Thạch Động. Điện Bà ở độ cao 350m, khu vực này có chùa Thượng (chùa Bà) và chùa Hang.
Điện Bà – thờ Bà Đen - Linh Sơn Thánh Mẫu. Có nhiều huyền thoại về Bà Đen như Sự tích Nàng Đênh, truyện Lý Thị Thiên Hương… được truyền tụng trong nhân dân (dù đã được viết thành sách hoặc dàn dựng thành phim, nhưng vẫn dựa vào truyền thuyết).
Truyện kể về một đôi trai tài, gái sắc đã nguyện ước đính hôn, nhưng giữa buổi loạn ly, chàng trai Lê Sĩ Triệt phải lên đường tòng quân giữ nước. Nàng Lý Thị Thiên Hương, người con quê hương xứ Trảng Bàng ở lại một dạ thủ tiết thờ chồng. Nàng Thiên Hương là người mộ đạo. Trong một ngày lên núi đi chùa lạy Phật nàng bị thát oan. Về sau nàng hiển linh luôn phù hộ cho nhân dân trong vùng được phước lành. Vua Gia Long khi lên ngôi tưởng nhớ chuyện được Bà mách bảo nên thoát nạn tại núi - Vua sai Tả quân Lê Văn Duyệt lên núi làm lễ sắc phong và tạc tượng Bà thờ ở một hang đá trên núi gọi là Điện Bà (Linh Sơn Tiên Thạch Động). Sắc phong đó bị thất lạc. Đến năm 1936 (Bảo Đại thập niên, tứ nguyệt, thập cửu nhật) đã tái phong sắc cho Bà.
Điện Bà được cải tạo từ một mái đá tự nhiên nhô ra tạo thành một hang động. Vòm mái cao 2,5m; cửa rộng 6m. Hai bên được xây gạch ốp sát vách đá. Ở giữa có xây cột gạch chống đỡ, vòm mái trước xây thêm tạo thành 2 lớp nhà điện dài 8m dùng để nơi phật tử chiêm bái và hành lễ. Trong động thờ cốt Bà (tượng Bà) và các tiên nữ.
Tháng giêng hàng năm thiện nam, tính nữ thập phương về lễ viếng Bà cầu tài, xin lộc. Đặc biệt, ngày mùng 5 tháng giêng hàng năm, ngày vía Bà có hàng chục vạn lượt người đến viếng lễ. Suốt trong năm mỗi ngày đều có người hành hương về núi viếng Bà, lạy phật.
Toàn bộ quần thể núi Bà rải rác có nhiều chùa, nhưng chỉ có ngôi chùa chính có quy mô lớn. Ngoài chùa Thượng (chùa Bà) còn có chùa Hạ, chùa Trung. Những ngôi chùa này đã được xây dựng từ lâu đời, nhưng qua các cuộc chiến tranh ác liệt, bom đạn tàn phá nên đổ nát. Những ngôi chùa hiện nay được xây dựng lại từ các năm 1995, 1997.
Từ những ngày đầu tiên xây dựng chùa có các vị tổ sư: Chủ tổ Thiệt Diệu, Tế Giác, Đại Cơ, Đạo Trung, Tánh, Thiền Hải Hiệp (nay còn tháp ở chùa). Tiếp đến là Thánh Thọ Phước Chí (tại vị 1871 - 1880). Tổ Trừng Tùng Chơn Thoại kiến thiết chùa phật, nhà giảng đường (tại vị 1880 - 1910). Tổ Tâm Hòa Chánh Khâm (tại vị 1910 - 1937) xây cất chùa tổ bằng đá (1922 - 1924), nhà tổ bằng đá (1937). Tổ Nguyên Cơ Giác Phú, Nguyên Cần Giác Hạnh lập tháp cho bổn sư và sư huynh (1939), Sư Nguyên Bộ Giác Ngọc (tự DiNa) trụ trì từ 1946 - 1957. Hòa Thượng Nguyên Chất Giác Điền (tại vị 1952 - 1957) thay mặt hàng năm lo liệu lễ vía Bà và khai trường hương, trường kì. Từ năm 1956, lập ra Hội núi Điện Bà do bác sĩ Nguyễn Văn Thọ giữ chức danh Hội trưởng.
Từ năm 1983, tỉnh Tây Ninh thành lập Ban Tổ chức Hội xuân Núi Bà hàng năm và Ban Quản lý di tích lịch sử văn hóa núi Bà Đen.
Cấu tạo địa chất bởi nhiều tầng đá tảng chồng lên nhau tạo ra nhiều hang động tự nhiên và một thảm động, thực vật phong phú đa dạng về sinh thái. Với đỉnh núi cao nhất Nam bộ, núi Bà Đen trở thành một vị trí chiến lược đặc biệt quan trọng, nên trong suốt 2 cuộc kháng chiến giải phóng dân tộc (1946 - 1975), lực lượng cách mạng và phản cách mạng đã giành giật nhau quyết liệt quả núi này.
Tháng 6/1946 lực lượng kháng chiến rút lên núi, thực dân Pháp đưa quân lên bao vây, cuộc chiến đấu tại dốc thượng làm tiêu hao nhiều binh lực Pháp. Chùa Trung đã từng làm nơi hội nghị của Chủ tịch Ủy ban Hành chánh kháng chiến các xã để trường kỳ kháng chiến. Suốt 15 năm kháng chiến chống Mỹ (1960 - 1975) nhiều đơn vị của cách mạng bám giữ núi Bà Đen. Đã có 7 lần tấn công căn cứ truyền tin của quân Mỹ trên đỉnh núi. Các căn cứ Huyện ủy Tòa Thánh. Dương Minh Châu, Liên đội 7 và nhiều đơn vị chủ lực đã bám núi đánh giặc – đến ngày 6/1/1975 toàn bộ núi Bà Đen được hoàn toàn giải phóng.
Núi Bà Đen là một quần thể di tích lịch sử - văn hóa và danh lam thắng cảnh nổi tiếng ở Nam bộ. Với hệ thống hang động và cảnh quan tự nhiên kết hợp kiến trúc tôn giáo đã tô điểm cho núi Bà Đen một nét đẹp thiên phú và nhân tạo, con người hòa quyện với thiên nhiên. Nó thật sự trở thành nơi trở về với cội nguồn đời sống tâm linh và du lịch sinh thái của dân tộc.


a. x2 - 2x
⇔ x(x - 2)
b. 3x - 6y
⇔ 3(x - 2y)
c. 5(x + 3y) - 15x(x + 3y)
⇔ (5 - 15x)(x + 3y)
d. 3(x - y) - 5x(y - x)
⇔ 3(x - y) + 5x(x - y)
⇔ (3 + 5x)(x - y)

Độ dài của chiều cao là:
12:2=6(cm)
=>Diện tích hình bình hành đó là:
12x6=72(cm2)
Đáp số:72 cm2

Đặt \(\sqrt{\dfrac{x^2}{x-3}}=a\left(a>=0\right)\)
Theo đề, ta có bất phương trình:
\(a^2>2a+8\)
=>(a-4)(a+2)>0
=>a-4>0
\(\Leftrightarrow\dfrac{x^2}{x-3}>16\)
\(\Leftrightarrow x^2-16x+48>0\)
\(\Leftrightarrow x\in R\)
Vậy: S=R\{3}

a.
Đường tròn có tâm \(\left\{{}\begin{matrix}x_I=2m\\y_I=-m-3\end{matrix}\right.\)
\(\Rightarrow x_I+2y_I=2m+2\left(-m-3\right)=-6\)
\(\Leftrightarrow x_I+2y_I+6=0\)
Hay quỹ tích tâm I của đường tròn là đường thẳng có pt: \(x+2y+6=0\)
b.
Gọi H là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}AH=\dfrac{1}{2}AB=3\\IH\perp AB\end{matrix}\right.\) \(\Rightarrow IH=d\left(I;d\right)\)
\(R=IA=\sqrt{\left(2m\right)^2+\left(-m-3\right)^2-\left(5m^2-6m-16\right)}=5\)
\(\Rightarrow IH=\sqrt{IA^2-AH^2}=4\)
\(d\left(I;d\right)=\dfrac{\left|3.2m-4\left(-m-3\right)+12\right|}{\sqrt{3^2+\left(-4\right)^2}}=4\)
\(\Leftrightarrow\left|10m+24\right|=20\Rightarrow\left[{}\begin{matrix}m=-\dfrac{2}{5}\\m=-\dfrac{22}{5}\end{matrix}\right.\)

\(\dfrac{1}{\sqrt{\dfrac{5}{7}}+\sqrt{\dfrac{5}{13}}+1}+\dfrac{1}{\sqrt{\dfrac{7}{13}}+\sqrt{\dfrac{7}{5}}+1}+\dfrac{1}{\sqrt{1\dfrac{6}{7}}+\sqrt{2\dfrac{3}{5}}+1}\\ =\dfrac{1}{\dfrac{\sqrt{5}}{\sqrt{7}}+\dfrac{\sqrt{5}}{\sqrt{13}}+\dfrac{\sqrt{5}}{\sqrt{5}}}+\dfrac{1}{\dfrac{\sqrt{7}}{\sqrt{13}}+\dfrac{\sqrt{7}}{\sqrt{5}}+\dfrac{\sqrt{7}}{\sqrt{7}}}+\dfrac{1}{\dfrac{\sqrt{13}}{\sqrt{7}}+\dfrac{\sqrt{13}}{\sqrt{5}}+\dfrac{\sqrt{13}}{\sqrt{13}}}\\ =\left(\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}\right)\cdot\dfrac{1}{\dfrac{1}{\sqrt{5}}+\dfrac{1}{\sqrt{7}}+\dfrac{1}{\sqrt{13}}}\\ =1\)