Tổng tất cả các nghiệm của phương trình
(x2 - 1)(x2 - 2)(x2 - 3)...(x2 - 2013)
mình đang gấp ai giúp với !!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 3:
$\Delta=2015^2-4.2013.2=2011^2$
Do đó pt có 2 nghiệm:
$x_1=\frac{2015+2011}{2.2013}=1$
$x_2=\frac{2015-2011}{2.2013}=\frac{2}{2013}$
Đáp án B.
Câu 4:
Theo định lý Viet, tổng các nghiệm của pt là:
$S=\frac{-b}{a}=\frac{-3}{1}=-3$
Đáp án B.

Xét \(\Delta=\text{}\)\(\left(-4m\right)^2-4\left(3m^2-3\right)\)\(=4m^2+12>0\forall m\)
=> Pt luôn có hai nghiệm pb
Theo viet \(\left\{{}\begin{matrix}x_1+x_2=4m\\x_1x_2=3m^2-3\end{matrix}\right.\)
\(P=\dfrac{2019}{\left|x_1-x_2\right|}\)\(\Leftrightarrow P^2=\dfrac{2019^2}{\left(x_1-x_2\right)^2}\)\(=\dfrac{2019^2}{\left(x_1+x_2\right)^2-4x_1x_2}\)\(=\dfrac{2019^2}{16m^2-4\left(3m^2-3\right)}\)
\(=\dfrac{2019^2}{4m^2+12}\le\dfrac{2019^2}{12}\)
\(\Rightarrow P\le\dfrac{2019}{\sqrt{12}}\)
\(\Rightarrow P_{max}=\dfrac{2019\sqrt{12}}{12}\Leftrightarrow m=0\)
Vậy m=0

a) Thay x=0 vào phương trình, ta được:
\(4\cdot0^2-2\cdot\left(2m+3\right)\cdot0+m+1=0\)
\(\Leftrightarrow m+1=0\)
hay m=-1
Áp dụng hệ thức Vi-et, ta có:
\(x_1+x_2=\dfrac{2\left(2m+3\right)}{4}\)
\(\Leftrightarrow x_1=\dfrac{2\cdot\left(-2+3\right)}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
Vậy: Khi m=-1 và nghiệm còn lại là \(x=\dfrac{1}{2}\)

Ta có : \(x^2-2\left(m-1\right)x+m^2+m+1=0\left(a=1;b=-2m+2;c=m^2+m+1\right)\)
\(\Delta=\left(-2m+2\right)^2-4\left(m^2+m+1\right)=4m^2+4-4m^2-4m-4=-4m< 0\)
Nếu \(-4m< 0\Leftrightarrow m>0\) chắc ĐK là vậy.
Theo hệ thức Vi et ta có : \(x_1+x_2=2m+2;x_1x_2=m^2+m+1\)
Theo bài ra ta có : \(x_1^2+x_2^2=4x_1x_2-2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-4x_1x_2=4x_1x_2-2\) Thay vao ta có pt mới :
\(\Leftrightarrow\left(2m+2\right)^2-4\left(m^2+m+1\right)=4\left(m^2+m+1\right)-2\)
\(\Leftrightarrow4m+4-4m^2-m-1=4m^2+4m+4-2\)
\(\Leftrightarrow3m+3-4m^2=4m^2+4m+2\)
\(\Leftrightarrow-m+1-8m^2=0\) Ta có : \(\left(-1\right)^2-4\left(-8\right)=1+32=33>0\)
\(x_1=\frac{1-\sqrt{33}}{-16};x_2=\frac{1+\sqrt{33}}{-16}\)
Tớ ngu ! tớ nhận.
Sửa từ dòng 4 trở lên.
\(\Leftrightarrow4m^2+4-4m^2-m-1=4m^2+4m+4-2\)
\(\Leftrightarrow3-m=4m^2+4m+2\)
\(\Leftrightarrow3-m-4m^2-4m-2=0\)
\(\Leftrightarrow1-5m-4m^2=0\)Ta có : \(\left(-5\right)^2-4\left(-4\right)=25+16=41>0\)
\(x_1=\frac{5-\sqrt{41}}{-4};x_2=\frac{5+\sqrt{41}}{-4}\)

=>(x1+x2)^2+x1x2=1
=>(-2m)^2+(-3)=1
=>4m^2=4
=>m=-1 hoặc m=1
Do a = 1 và c = -3
⇒ a và c trái dấu
⇒ Phương trình luôn có hai nghiệm phân biệt
Theo Viét, ta có:
x₁ + x₂ = -2m
x₁x₂ = -3
Lại có:
x₁² + x₂² + 3x₁x₂ = 1
⇔ x₁² + 2x₁x₂ + x₂² + x₁x₂ = 1
⇔ (x₁ + x₂)² + x₁x₂ = 1
⇔ (-2m)² - 3 = 1
⇔ 4m² = 4
⇔ m² = 1
⇔ m = -1 hoặc m = 1
Vậy m = -1; m = 1 thì phương trình đã cho có hai nghiệm phân biệt x₁, x₂ thỏa mãn: x₁² + x₂² + 3x₁x₂ = 1

a) Với m = 1 phương trình trở thành:
x 2 + 4x + 4 = 0 ⇔ (x + 2 ) 2 = 0 ⇔ x = -2
Vậy x = -2
b) Ta có: Δ' = m 2 - 5m + 4
Phương trình có hai nghiệm phân biệt
⇔ Δ' > 0 ⇔
m
2
- 5m + 4 > 0 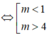
Do x1 < x2 < 1
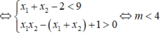

\(\Delta'=\left(m+1\right)^2-\left(m^2+2m\right)=1>0\)
\(\Rightarrow\) Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=m+1-1=m\\x_2=m+1+1=m+2\end{matrix}\right.\)
\(\left|x_1\right|=3\left|x_2\right|\Leftrightarrow\left|m\right|=3\left|m+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3m+6=-m\\3m+6=m\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{3}{2}\\m=-3\end{matrix}\right.\)
tổng nghiệm bằng 0 nhé, vì \(x^2=a\left(a>0\right)\Leftrightarrow\orbr{\begin{cases}x=\sqrt{a}\\x=-\sqrt{a}\end{cases}}\)
do đó nghiệm đối nhau từng cặp, nên tổng bằng 0