Cho \(\Delta ABC\) dều. Lấy các điểm \(M\in AB,N\in AC,P\in BC\) sao cho \(S_{MNA}=S_{NCP}=S_{BMP}\). Chứng minh \(\Delta ABC\) đều.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 2 2022
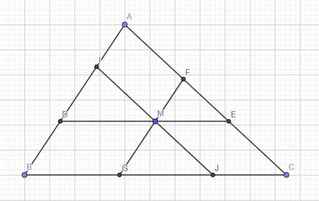
\(\left\{{}\begin{matrix}\widehat{MGJ}=\widehat{B}\left(\text{đồng vị}\right)\\\widehat{MJG}=\widehat{C}\left(\text{đồng vị}\right)\end{matrix}\right.\) \(\Rightarrow\Delta MGJ\sim\Delta ABC\) theo tỉ số \(k_1=\dfrac{GJ}{BC}\)
\(\Rightarrow S_{ABC}.k_1^2=S_{MGJ}\Rightarrow k_1=\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}=\dfrac{GJ}{BC}\) (1)
Tương tự: \(\dfrac{DM}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\), mà BDMG là hbh (2 cặp cạnh đối song song)
\(\Rightarrow DM=BG\Rightarrow\dfrac{BG}{BC}=\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}\) (2)
Tương tự: \(\dfrac{CJ}{BC}=\sqrt{\dfrac{S_{FME}}{S_{ABC}}}\) (3)
Cộng vế (1);(2);(3) \(\Rightarrow\sqrt{\dfrac{S_{MGJ}}{S_{ABC}}}+\sqrt{\dfrac{S_{IDM}}{S_{ABC}}}+\sqrt{\dfrac{S_{FME}}{S_{ABC}}}=\dfrac{BG+GJ+JC}{BC}=1\)
\(\Rightarrow S_{ABC}=\left(\sqrt{S_{MGJ}}+\sqrt{S_{IDM}}+\sqrt{S_{FME}}\right)^2\le3\left(S_{MGJ}+S_{IDM}+S_{FME}\right)\)
Mà \(S_{MGJ}+S_{IDM}+S_{FME}=S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\)
\(\Rightarrow S_{ABC}\le3\left[S_{ABC}-\left(S_{AIMF}+S_{BGMD}+S_{CEMJ}\right)\right]\)
\(\Rightarrow S_{AIMF}+S_{BGMD}+S_{CEMJ}\le\dfrac{2}{3}S_{ABC}\)
AH
Akai Haruma
Giáo viên
9 tháng 4 2018
Lời giải:
a)
Vì $M, N$ lần lượt là trung điểm của $AB,AC$ nên:
\(\frac{AM}{AB}=\frac{AN}{AC}=\frac{1}{2}\)
Xét tam giác $AMN$ và $ABC$ có:
\(\left\{\begin{matrix} \text{chung góc A}\\ \frac{AM}{AB}=\frac{AN}{AC}\end{matrix}\right.\Rightarrow \triangle AMN\sim \triangle ABC\) (c.g.c)
b)
Áp dụng định lý Pitago cho tam giác vuông $ABC$:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{9^2+12^2}=15\) (cm)
Ta có:
\(\frac{AB.AC}{2}=S_{ABC}=\frac{AH.BC}{2}\)
\(\Rightarrow AH=\frac{AB.AC}{BC}=\frac{9.12}{15}=7,2\) (cm)
c)
Vì \(NP\parallel AB\) nên áp dụng định lý Ta-lét ta có:
\(\frac{NP}{AB}=\frac{CN}{CA}=\frac{1}{2}\Rightarrow NP=\frac{AB}{2}; NC=\frac{AC}{2}\)
Mặt khác, \(NP\parallel AB, AB\perp AC\Rightarrow NP\perp AC\)
Do đó:
\(S_{NPC}=\frac{NP.NC}{2}=\frac{\frac{AB}{2}.\frac{AC}{2}}{2}=\frac{AB.AC}{8}\)
\(S_{ABC}=\frac{AB.AC}{2}\)
\(\Rightarrow \frac{S_{NPC}}{S_{ABC}}=\frac{AB.AC}{8}: \frac{AB.AC}{2}=\frac{1}{4}\)
có tam giác ABC đều (gt)
=> góc A = góc B = góc C (đn) (1)
AB = AC = BC
AB = BM + MA
AC = AN + NC
BC = BE + CE
mà BE = CN = AM (gt) (2)
=> BM = AN = CE (3)
(1)(2)(3) => tam giác AMN = tam giác CNE = tam giác BEM (c - g - c)
=> MN = NE = EM
=> tam giác MEN đều