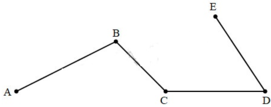
tính độ dài đường gấp khúc sau: 3cm 3cm 3cm 3cm A B C D E ...
Đọc tiếp
tính độ dài đường gấp khúc sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LM
9 tháng 4 2020
Giải
Vì AB=1/2 BC mà AC =3cm
Suy ra BC=1/2*3=6cm
Vì BCD dài hơn ABC 5cm mà ABC =3+6=9cm
Suy ra BCD= 9+5=14cm
Vậy độ dài đường gấp khúc ABCD là 3+14=17cm
8 tháng 5 2021
Bộ ba độ dài nào sau đây có thể là độ dài 3 cạnh của một Tam giác:
A. 3cm;3cm;5cm. B. 2cm;3cm;5cm C.1cm;2cm;5cm D.1cm;2cm;3cm
Hok tốt.
17 tháng 4 2023
`A. 3 cm, 3cm, 4cm`
Theo bất đẳng thức trong tam giác, ta có:
`3+3>4`
`->`\(\text{ Bộ ba độ dài này là độ dài 3 cạnh của 1 tam giác (k t/m)}\)
`B. 6cm, 10cm, 8 cm`
Theo bất đẳng thức trong tam giác, ta có:
`6+8>10`
`->`\(\text{ Bộ ba độ dài này là độ dài 3 cạnh của 1 tam giác (k t/m)}\)
`C.3cm, 4cm, 5cm`
Theo bất đẳng thức trong tam giác, ta có:
`3+4>5`
`->`\(\text{ Bộ ba độ dài này là độ dài 3 cạnh của 1 tam giác (k t/m)}\)
`D. 4cm, 8cm, 12cm`
Theo bất đẳng thức trong tam giác, ta có:
`4+8=12`
`->`\(\text{ Bộ ba độ dài này không phải là độ dài 3 cạnh của 1 tam giác (t/m)}\)
Xét các đáp án trên `-> D.`
A
5 tháng 3 2023
Xét đáp án \(A,\) ta có:
\(2^2+3^2=13\ne5^2=25\) (loại)
Xét đáp án \(B,\) ta có:
\(2^2+4^2=20\ne5^2=25\) (loại)
Xét đáp án \(C,\) ta có:
\(3^2+4^2=25\ne6^2=36\) (loại)
Xét đáp án \(D,\) ta có:
\(3^2+4^2=5^2=25\) (nhận) (định lí pitago đảo)
Vậy các đáp án \(A,B,C\) là bộ ba độ dài không tạo thành một tam giác.
TA
15 tháng 6 2021
Áp dụng định lí Pytago:
`BC^2=AB^2+AC^2`
`<=>BC^2=3^2+4^2`
`<=>BC=5(cm)`
AM là đường trung tuyến của `\DeltaABC`
`=> AM = (BC)/2 = 5/2 (cm)`
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2022
3cm, 3cm, 5cm có thể là độ dài 3 cạnh của 1 tam giác
C đúng
CM
16 tháng 2 2019
Nếu đoạn thẳng CD = 3cm thì độ dài đường gấp khúc ABCD là 10cm (Vì AB + BC + CD = 5 + 2 + 3 = 10 cm).