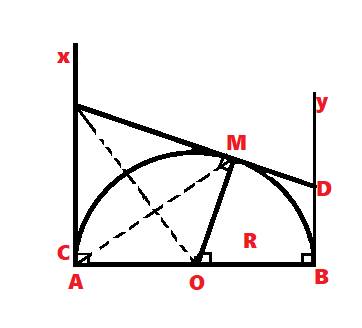
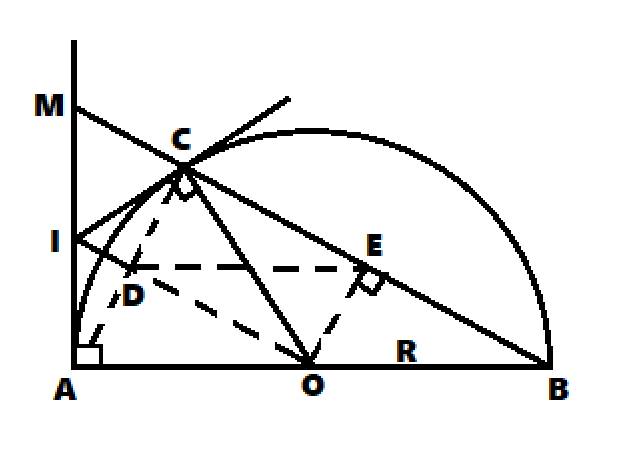
Cho nửa đường tròn tâm O, đường kính AB. Kẻ các tiếp tuyến Ax,By cùng phía với nửa đường tròn. Vẽ bán kính OE (E thuộc 1/2(O),E khác A,B). Tiếp tuyến của nửa đường tròn tại E cắt Ax, By lần lượt tại C và D.
a, Cm AC+BD=CD
b, góc COD = 90°
c, Gọi I là giao của OC và EA, K là giao của OD và BE. Tứ giác EIOK là hình gì? Vì sao?
d, Xác định vị trí của bán kính OE để tứ giác EIOK là hình vuông.
GIÚP MÌNH NHÉ!