Cho tam giác ABC có trung tuyến AM, trọng tâm G. Biết diện tích tam giác ABC là 120cm2, khi đó diện tích tam giác GMC là ...cm2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
2 tháng 1 2017
Tương tự 1B. Ta được:
S G A B = S G B C = S G C A = 1 3 S A B C
Þ SGBC = 10cm2
CM
26 tháng 2 2019
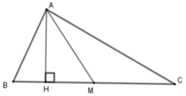
Kẻ AH ⊥ BC tại H. Ta có SABC = 1 2 AH. BC
SAMC = 1 2 AH.MC
Mà AM là đường trung tuyến nên M là trung điểm của BC => BC = 2AM
Từ đó SABC = 1 2 AH. BC = SABC = 1 2 AH. 2MC = 2SAMC
Suy ra SAMC = 1 2 SABC = 1 2 .60 = 30 cm2
Vậy SAMC = 30 cm2
Đáp án cần chọn là: A
CM
30 tháng 3 2019
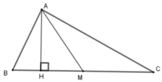
Kẻ AH ⊥ BC tại H. Ta có SABC = 1 2 AH. BC; SAMC = 1 2 AH.MC
Mà AM là đường trung tuyến nên M là trung điểm của BC => BC = 2AM
Từ đó SABC = 1 2 AH. BC = SABC = 1 2 AH. 2MC = 2SAMC
Suy ra SAMC = 1 2 SABC = 1 2 .40 = 20 cm2
Vậy SAMC = 20 cm2
Đáp án cần chọn là: C
11 tháng 4 2022
*MO//BN (O thuộc AC).
\(\dfrac{AK}{AM}=\dfrac{1}{2}\Rightarrow\)K là trung điểm AM.
-△AMO có: K là trung điểm AM, KN//MO \(\Rightarrow\)N là trung điểm AO.
-△BNC có: MO//BN, M là trung điểm BC \(\Rightarrow\)O là trung điểm NC.
\(\Rightarrow AN=ON=OC=\dfrac{1}{3}AC\)
\(\dfrac{S_{AKN}}{S_{ABC}}=\dfrac{S_{AKN}}{S_{AMC}}.\dfrac{S_{AMC}}{S_{ABC}}=\dfrac{AN}{AC}.\dfrac{MC}{BC}=\dfrac{1}{3}.\dfrac{1}{2}=\dfrac{1}{6}\)
\(\Rightarrow S_{AKN}=\dfrac{S_{ABC}}{6}=\dfrac{60}{6}=10\left(cm^2\right)\)