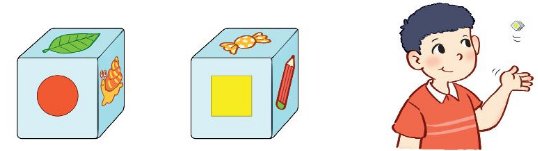
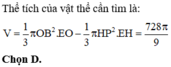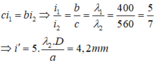Hai bạn Kim và Sam ngồi đối diện nhau và cùng quan sát một con xúc sắc ở giữa. Mỗi bạn chỉ có thể nhìn thấy mặt trên cùng và hai trong bốn mặt bên của con xúc sắc (hai mặt bên mà hai bạn quan sát được không có mặt nào trùng nhau). Kim đếm được tổng cộng 10 chấm ở ba mặt nhìn thấy. Sam đếm được tổng cộng 14 chấm ở ba mặt mình nhìn thấy. Hỏi mặt dưới cùng của con xúc sắc có bao nhiêu chấm tròn, biết rằng tổng số chấm của hai mặt đối nhau luôn bằng 7?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Không thể xảy ra
b) Có thể xảy ra
c) Chắc chắn xảy ra
d) Có thể xảy ra

Mặt trên của con xúc xắc có thể xuất hiện mặt: chấm tròn màu đỏ hoặc chiếc lá hoặc bàn tay hoặc cái kẹo hoặc hình vuông hoặc chiếc bút chì.

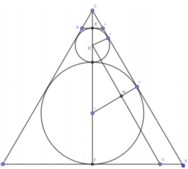
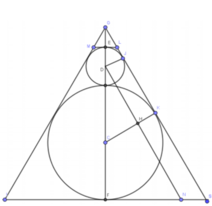
Gọi tâm của hai đường tròn trong (N) là C và D. Ta có GS là tiếp tuyến chung của hai đường tròn tại K và J. Khi đó: D J ⊥ G S C K ⊥ G S
Kẻ D N / / G S ( N ∈ I S ) , khi đó DHKJ là hình chữ nhật nên HK=DJ=1 cm, do đó ta có CH=2 cm.
Ta có ∆ D H C đồng dạng ∆ G J D nên D J C H = G D C D
⇒ D G = D J . C D C H = 1 . 4 2 = 2 cm từ đó suy ra GF = 9 cm.
Ta có ∆ D H C đồng dạng ∆ G F S ⇒ G S D C = G F D H
⇒ G S = D C . G F D H = D C . G F D C 2 - C H 2 = 6 3 cm
⇒ F S = G S 2 - G F 2 = 3 3 cm.
Vì ∆ G E L đồng dạng ∆ G F S nên E L F S = G E G F
⇒ E L = G E . F S G F = 1 . 3 3 9 = 3 3
Vì (N) là khói nón cụt nên:
V N = 1 3 E L 2 + F S 2 + E L . F S E F = 728 π 9
Chọn đáp án D.

Đáp án D
Khoảng vân là:
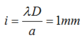
Vân sáng có vị trí x = ki
Vân tối có vị trí (k’ + 1/2) i
Vậy khoảng cách từ vân sáng bậc 1 và vân tối thứ 3 ở cùng 1 phía so với vân trung tâm là :
![]()

Phương pháp: áp dụng công thức tính khoảng vân và công thức xác định vị trí vân sáng
Cách giải: Khoảng vân là: i = λ D a = 1 m m
Vân sáng có vị trí x = ki
Vân tối có vị trí (k’ + 1/2) i
Vậy khoảng cách từ vân sáng bậc 1 và vân tối thứ 3 ở cùng 1 phía so với vân trung tâm là
![]()
Đáp án D

Đáp án D
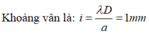
Vân sáng có vị trí x = ki
Vân tối có vị trí (k’ + 1/2) i
Vậy khoảng cách từ vân sáng bậc 1 và vân tối thứ 3 ở cùng 1 phía so với vân trung tâm là:
![]()

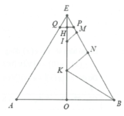
HD: Giả sử thiết diện là hình thang ABPQ
Gọi I, K lần lượt là tâm của đường tròn nhỏ và to.
Gọi M, N là hình chiếu của I, K lên một cạnh bên, điểm