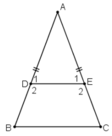
Cho tam giác ABC cân tại A.gọi tam giác D,E lần lượt là trung điểm của các cạnh AB,AC
a)Chứng minh bdec là hình thang cân
b)tính các góc của hình thang cân đó , biết rằng bac=50
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta xét: Tam giác ADE có: AD = AE
=> Tam giác ADE cân tại A
\(\Rightarrow\widehat{AED}=\widehat{ACB}\)
=> DE//BC
Ta xét: Tứ giác DECB có: DE//BC
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
=> BDEC là hình thang cân
b) \(\widehat{ABC}=\frac{1}{2}\left(180^o-50^o\right)=65^o\)
\(\widehat{ACB}=\widehat{ABC}=65^o\)
\(\widehat{DEC}=180^o-65^o=115^o\)
\(\widehat{EDB}=\widehat{EDC}=115^o\)

Mà hai góc ở vị trí đồng vị ⇒ DE // BC
⇒ Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
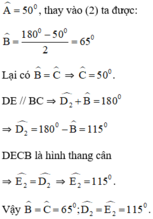

a) Ta có AD = AE nên ∆ADE cân
Do đó ˆD1= ˆE1
Trong tam giác ADE có: D1^ + ˆE1 + ˆA^=1800
Hay 2ˆD1 = 1800 - ˆA
ˆD1 = 180 độ −ˆA/2
Tương tự trong tam giác cân ABC ta có ˆB= 180−ˆA/2
Nên ˆD1 = ˆB ( hai góc đồng vị.)
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có ˆB = ˆC
Nên BDEC là hình thang cân.
b) Với ˆA=500
Ta được ˆB = ˆC = 180−ˆA/2= 180-50/2=65 độ
ˆD2=ˆE2=1800 - ˆB= 1800 - 650=1150
a) Ta có : AD = AE => \(\Delta ADE\)cân
\(\Rightarrow\widehat{D_1}=\widehat{E_1}\)
\(\Delta ADE\)có : \(\widehat{A}+\widehat{D_1}+\widehat{E_1}=180^o\)
Mà \(\widehat{D_1}=\widehat{E_1}\)nên \(\widehat{A}+2.\widehat{D_1}=180^o\)
\(\Rightarrow2.\widehat{D_1}=180^o-\widehat{A}\Rightarrow\widehat{D_1}=\frac{180^o-\widehat{A}}{2}\left(1\right)\)
Tam giác ABC có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}=\widehat{C}\)( Vì tam giác ABC cân tại A )
\(\Rightarrow\widehat{A}+2.\widehat{B}=180^o\Rightarrow\widehat{B}=\frac{180^o-\widehat{A}}{2}\left(2\right)\)
Từ (1)(2) => \(\widehat{D_1}=\widehat{B}\)
Mà hai góc ở vị trí đồng vị => DE // BC
=> Tứ giác DECB là hình thang.
Mà hai góc ở đáy B và C bằng nhau nên hình thang DECB là hình thang cân.
b)
\(\widehat{A}=50^o\)thay vào (2) ta được :
\(\widehat{B}=\frac{180^o-50^o}{2}=65^o\)
Ta lại có : \(\widehat{B}=\widehat{C}\Rightarrow\widehat{C}=50^o\)
\(DE//BC\Rightarrow\widehat{D_1}+\widehat{B}=180^o\)
\(\Rightarrow\widehat{D_1}=180^o-\widehat{B}=115^o\)
DECB là hình thang cân
\(\Rightarrow\widehat{E_2}=\widehat{D_2}\Rightarrow\widehat{E_2}=115^o\)
Vậy : \(\widehat{B}=\widehat{C}=65^o\); \(\widehat{D_2}=\widehat{E_2}=115^o\)

Hình vẽ:

a)Xét \(\Delta ADE\) có:AD=AE(gt)
\(\Rightarrow\Delta ADE\) cân tại A
\(\Rightarrow\widehat{AED}=\dfrac{180^0-\widehat{A}}{2}\) (1)
Ta lại có:\(\Delta ABC\) cân tại A
\(\Rightarrow\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{AED}=\widehat{ACB}\)
\(\Rightarrow\) DE song song với BC
Xét tứ giác DEBC có:
DE song song với BC
\(\widehat{ABC}=\widehat{ACB}\) ( 2 góc đáy của tam giác ABC cân tại A)
\(\Rightarrow\) BDEC là hình thang cân
\(\Rightarrow\widehat{BDE}=\widehat{CED}\)
b) Theo câu a có:\(\widehat{ACB}=\dfrac{180^o-\widehat{A}}{2}=\dfrac{180^o-50^o}{2}=60^0\)
mà \(\widehat{ABC}=\widehat{ACB}\) ( câu a) nên \(\widehat{ABC}=60^o\)
Vì DE song song với BC\(\Rightarrow\) góc DEC+ góc BCE=180o
=>góc DEC+60o =180o
=>góc DEC=120o mà \(\widehat{BDE}=\widehat{CED}\)
=>BDE=120o

a) Xét ΔABC có
D là trung điểm của AB(gt)
E là trung điểm của AC(gt)
Do đó: DE là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
Suy ra: DE//BC và \(DE=\dfrac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)
Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang có hai đáy là DE và BC(Định nghĩa hình thang)
Hình thang BDEC(BC//DE) có \(\widehat{B}=\widehat{C}\left(=60^0\right)\)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
Ta có: \(DE=\dfrac{BC}{2}\)(cmt)
\(BD=\dfrac{1}{2}AB\)(D là trung điểm của AB)
\(EC=\dfrac{1}{2}AC\)(E là trung điểm của AC)
mà BC=AB=AC(ΔABC đều)
nên DE=BD=EC
Vậy: BDEC là hình thang cân có đáy nhỏ bằng cạnh bên
b) Ta có: \(DE=BD=EC=\dfrac{AB}{2}\)(cmt)
nên DE=BC=EC=3(cm)
Chu vi hình thang BDEC là:
C=DE+DB+EC+BC=3+3+3+6=15(cm)

a) Ta có AD = AE nên ∆ADE cân
Do đó =
Trong tam giác ADE có: +
+
=1800
Hay 2 = 1800 -
=
Tương tự trong tam giác cân ABC ta có =
Nên =
là hai góc đồng vị.
Suy ra DE // BC
Do đó BDEC là hình thang.
Lại có =
Nên BDEC là hình thang cân.
b) Với =500
Ta được =
=
=
= 650
=1800 -
= 1800 - 650=1150

a) Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(AB=AC;AD=AE\right)\)
D\(\in\)AB(gt)
E\(\in\)AC(gt)
Do đó: DE//BC(Định lí Ta lét đảo)
Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang(Định nghĩa hình thang)
Hình thang BDEC(DE//BC) có \(\widehat{B}=\widehat{C}\)(ΔABC cân tại A)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)