Cho A = x2 + 4x , x thuộc N
- Tìm x để A bằng 12
- Tìm x để A là số nguyên tố
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LT
1
Những câu hỏi liên quan
NT
0
PT
1
11 tháng 7 2016
a) 3x + 7x = x .(3 + 7) = x . 10
Với x thuộc N thì 3x + 7x luôn có ước là 10 => 3x + 7x chia hết cho 10 => 3x + 7x chia hết cho 2 và 5 => 3x + 7x có ít nhất 3 ước là 1; 2; 5, không là số nguyên tố
Vậy không tìm được giá trị x thỏa mãn
b) 7x - 4x = 3x
+ Với x = 0 => 7x - 3x = 0 - 0 = 0, không là số nguyên tố, loại
+ Với x = 1 => 7x - 4x = 7 - 4 = 3, là số nguyên tố, chọn
+ Với x > 1 thì 7x - 4x sẽ có ít nhất 3 ước là 1 ; x; 3, không là số nguyên tố, loại
Vậy x = 1
Ủng hộ mk nha ^_-
DH
0
CM
22 tháng 2 2019
Chọn B.
Phương pháp:
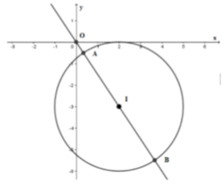
Biến đổi đẳng thức đã cho để đưa về dạng phương trình đường tròn (C) tâm I bán kính R.
Từ đó ta đưa bài toán về dạng bài tìm M x ; y ∈ C để O M - a lớn nhất hoặc nhỏ nhất.
Xét các trường hợp xảy ra để tìm a.
Cách giải:
H
10 tháng 4 2021
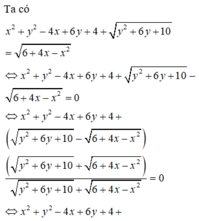
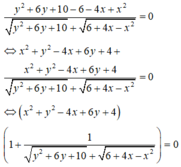
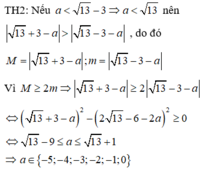
\(A=\dfrac{4x-1}{x+2}=\dfrac{4\left(x+2\right)-9}{x+2}=4-\dfrac{9}{x+2}\)
Để A nguyên mà 4 nguyên
\(\Leftrightarrow x+2\inƯ\left(9\right)=\left\{1;-1;3;-3;9;-9\right\}\\ \Leftrightarrow x\in\left\{-1;-3;1;-5;7;-11\right\}\)
10 tháng 4 2021
A=(4x+8-9)/(x+2)=2- 9/(x+2)
A€Z <=> 9 chia hết (x+2)
<=> x+2 € Ư(9)={±1,±3,±9}
<=> x€{...}
KH đk
VD
0
Lời giải:
$A=x^2+4x=12$
$\Leftrightarrow x^2+4x-12=0$
$\Leftrightarrow (x^2+6x)-(2x+12)=0$
$\Leftrightarrow x(x+6)-2(x+6)=0$
$\Leftrightarrow (x+6)(x-2)=0$
$\Leftrightarrow x+6=0$ hoặc $x-2=0$
$\Leftrightarrow x=-6$ hoặc $x=2$
----------------------
Để $A=x(x+4)$ là số nguyên tố thì phải có 1 trong 2 thừa số $x,x+4$ bằng 1, thừa số còn lại là số nguyên tố.
Vì $x<x+4$ nên $x=1$
Khi đó: $A=x(x+4)=1(1+4)=5$ là snt (thỏa mãn)
Vậy $x=1$