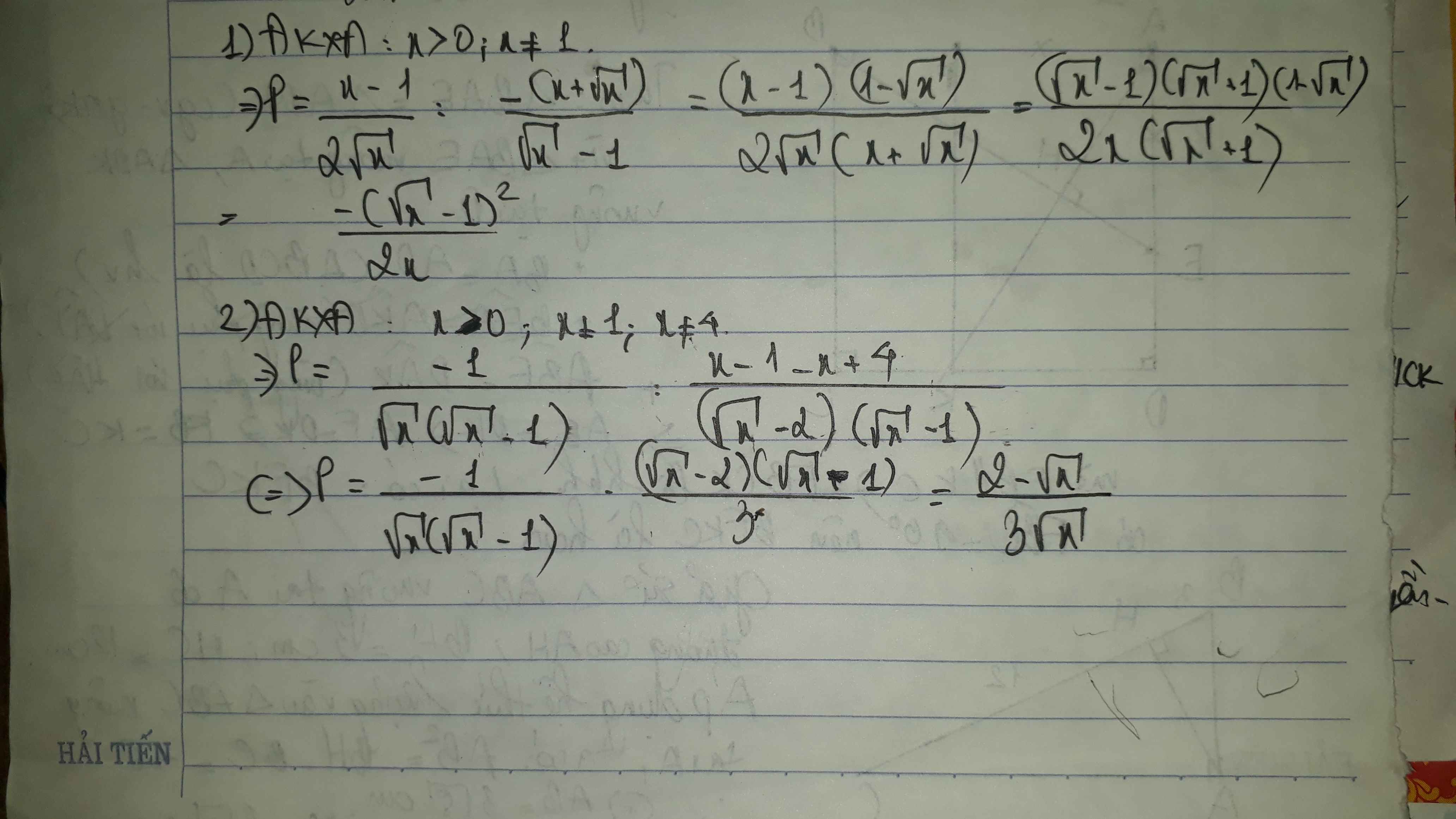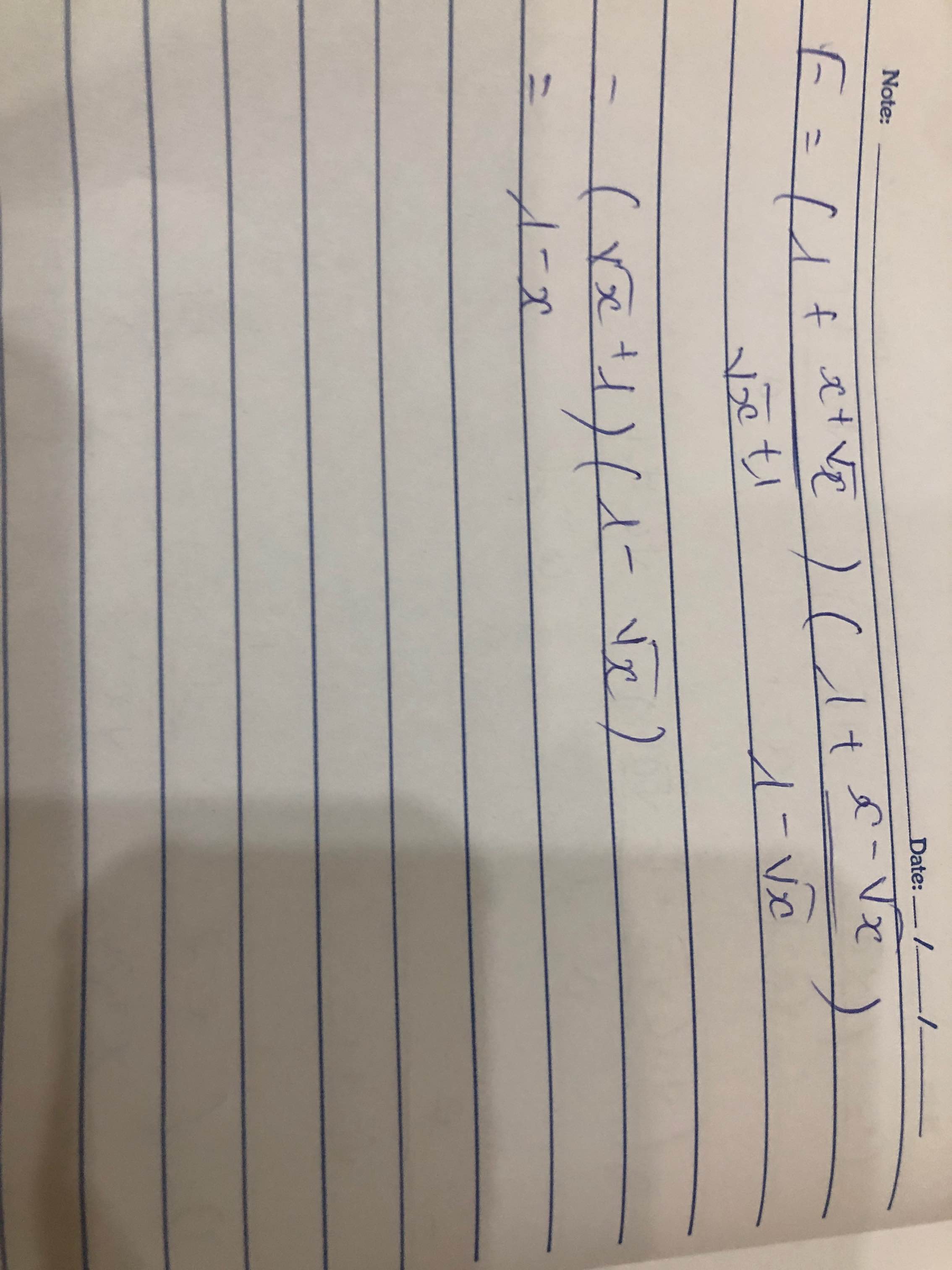rút gọn E=\(\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+4\sqrt{x}\right):\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
5 tháng 9 2023
\(E=\left(\dfrac{x\sqrt{x}}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right)+\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}+\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\right)\) (ĐK: \(x\ne1;x>0\))
\(E=\left[\dfrac{\left(\sqrt{x}\right)^3-1^3}{x-\sqrt{x}}-\dfrac{\left(\sqrt{x}\right)^3+1^3}{x+\sqrt{x}}\right]+\left[\dfrac{x}{\sqrt{x}}-\dfrac{1}{\sqrt{x}}\right]\left[\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\)
\(E=\left[\dfrac{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\left(\sqrt{x}+1\right)\left(x-\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\right]+\dfrac{x-1}{\sqrt{x}}\cdot\dfrac{\left(\sqrt{x}+1\right)^2+\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(E=\left(\dfrac{x+\sqrt{x}+1}{\sqrt{x}}-\dfrac{x-\sqrt{x}+1}{\sqrt{x}}\right)+\dfrac{\left(\sqrt{x}\right)^2-1^2}{\sqrt{x}}\cdot\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(E=\dfrac{x+\sqrt{x}+1-x+\sqrt{x}-1}{\sqrt{x}}+\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}}\cdot\dfrac{2x+2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(E=\dfrac{2\sqrt{x}}{\sqrt{x}}+\dfrac{2x+2}{\sqrt{x}}\)
\(E=\dfrac{2x+2\sqrt{x}+2}{\sqrt{x}}\)
5 tháng 9 2023
https://hoc24.vn/cau-hoi/rut-gon-cac-bieu-thuc-sau21-a-leftdfracxsqrtx-1x-1-dfracx-1sqrtx-1right-leftsqrtx-dfracsqrtxsqrtx-1right-22-a-leftdfracxsqrtx.8357393071878
14 tháng 8 2021
a: Ta có: \(E=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+4\sqrt{x}\right):\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)\)
\(=\left(\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+4\sqrt{x}\right):\left(\dfrac{x-1}{\sqrt{x}}\right)\)
\(=\left(\dfrac{4\sqrt{x}+4\sqrt{x}\left(x-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\sqrt{x}}{x-1}\)
\(=\dfrac{4x^2}{\left(x-1\right)^2}\)
14 tháng 8 2021
b: Để E=2 thì \(4x^2=2\left(x-1\right)^2\)
\(\Leftrightarrow4x^2-2x^2+4x-2=0\)
\(\Leftrightarrow2x^2+4x-2=0\)
\(\Leftrightarrow x^2+2x-1=0\)
\(\Leftrightarrow\left(x+1\right)^2=2\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\sqrt{2}-1\\x=\sqrt{2}-1\end{matrix}\right.\)
c: Ta có: \(x=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{10}-\sqrt{6}\right)\cdot\sqrt{4-\sqrt{15}}\)
\(=\left(4+\sqrt{15}\right)\cdot\left(\sqrt{5}-\sqrt{3}\right)^2\)
\(=\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\)
\(=2\)
Thay x=2 vào E, ta được:
\(E=\dfrac{4\cdot2^2}{1}=16\)
2 tháng 11 2021
\(1,\\ a,E=\dfrac{x-2\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\left(\sqrt{x}-1\right)^2}{\sqrt{x}\left(\sqrt{x}-1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}}\\ b,E>0\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}}>0\Leftrightarrow\sqrt{x}-1>0\left(\sqrt{x}>0\right)\\ \Leftrightarrow x>1\\ 2,\\ a,B=\dfrac{x-\sqrt{x}+\sqrt{x}+1-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\left(\sqrt{x}+1\right)\\ B=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\\ b,B=2\Leftrightarrow\sqrt{x}-1=2\left(\sqrt{x}+1\right)\\ \Leftrightarrow\sqrt{x}-1=2\sqrt{x}+2\\ \Leftrightarrow\sqrt{x}=-3\Leftrightarrow x\in\varnothing\)
25 tháng 1 2022
1: \(D=\dfrac{x+\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}+1}\)
2: \(\Leftrightarrow D=\dfrac{4\sqrt{x}+12-x+\sqrt{x}-13}{\sqrt{x}+3}\cdot\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
\(\Leftrightarrow D=\dfrac{-x+5\sqrt{x}-1}{\sqrt{x}+3}\cdot\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
\(\Leftrightarrow\dfrac{-x+5\sqrt{x}-1}{\sqrt{x}+3}\cdot\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\cdot\dfrac{\sqrt{x}+1}{x+\sqrt{x}+1}=1\)
\(\Leftrightarrow\left(-x+5\sqrt{x}-1\right)\left(2\sqrt{x}+1\right)=\left(x+\sqrt{x}+1\right)\left(\sqrt{x}+3\right)\)
\(\Leftrightarrow-2x\sqrt{x}-x+10x+5\sqrt{x}-2\sqrt{x}-1=x\sqrt{x}+3x+x+3\sqrt{x}+\sqrt{x}+3\)
\(\Leftrightarrow-2x\sqrt{x}+9x-3\sqrt{x}-1=x\sqrt{x}+4x+4\sqrt{x}+3\)
\(\Leftrightarrow-3x\sqrt{x}+5x-7\sqrt{x}-4=0\)
Bạn xem lại đề nhé, nghiệm rất xấu
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
1. ĐKXĐ: $x>0; x\neq 9$
\(A=\frac{\sqrt{x}+3+\sqrt{x}-3}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{\sqrt{x}}=\frac{2\sqrt{x}}{(\sqrt{x}-3)(\sqrt{x}+3)}.\frac{\sqrt{x}-3}{\sqrt{x}}=\frac{2}{\sqrt{x}+3}\)
AH
Akai Haruma
Giáo viên
17 tháng 7 2021
2. ĐKXĐ: $x\geq 0; x\neq 4$
\(B=\left[\frac{\sqrt{x}(\sqrt{x}+2)+\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)}+\frac{6-7\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}\right](\sqrt{x}+2)\)
\(=\frac{x+3\sqrt{x}-2+6-7\sqrt{x}}{(\sqrt{x}-2)(\sqrt{x}+2)}.(\sqrt{x}+2)=\frac{x-4\sqrt{x}+4}{\sqrt{x}-2}=\frac{(\sqrt{x}-2)^2}{\sqrt{x}-2}=\sqrt{x}-2\)
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
1.
\(Q=\left[\frac{\sqrt{x}+2}{(\sqrt{x}+1)^2}-\frac{\sqrt{x}-2}{(\sqrt{x}-1)(\sqrt{x}+1)}\right].\sqrt{x}(\sqrt{x}+1)\)
\(=\frac{\sqrt{x}(\sqrt{x}+2)}{\sqrt{x}+1}-\frac{\sqrt{x}(\sqrt{x}-2)}{\sqrt{x}-1}\)
\(=\frac{\sqrt{x}(\sqrt{x}+2)(\sqrt{x}-1)-\sqrt{x}(\sqrt{x}-2)(\sqrt{x}+1)}{(\sqrt{x}-1)(\sqrt{x}+1)}=\frac{2x}{x-1}\)
AH
Akai Haruma
Giáo viên
6 tháng 8 2021
2.
\(A=\left[\frac{\sqrt{x}+2-(\sqrt{x}-2)}{(\sqrt{x}-2)(\sqrt{x}+2)}-\frac{4\sqrt{x}}{x-4}\right].\frac{x-4}{\sqrt{x}+1}\)
\(=\left(\frac{4}{x-4}-\frac{4\sqrt{x}}{x-1}\right).\frac{x-4}{\sqrt{x}+1}=\frac{4(1-\sqrt{x})}{x-4}.\frac{x-4}{\sqrt{x}+1}=\frac{4(1-\sqrt{x})}{\sqrt{x}+1}\)
20 tháng 12 2022
\(=\dfrac{x+\sqrt{x}-3\sqrt{x}+1}{x-1}:\dfrac{x+2\sqrt{x}+1-4\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)