Giải giúp mình nha mn :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 12 D là cửa hàng tạp hóa mà. nên câu đó chọn A
15 thì insisted that + V nguyên ko to nên câu này chọn A


Lời giải:
a. Mẹ An mua thực phẩm hết số tiền là:
$3\times 120000+4\times 50000+20\times 3500+220000=850000$ (đồng)
b. Mẹ An mua thực phẩm và khẩu trang hết:
$850000+2\times 35000=920000$ (đồng)

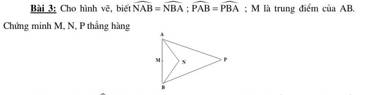
Xét tam giác NAB cân tại N, có M là trung điểm của AB suy ra NM vuông góc với AB (1)
Xét tam giác APB cân tại P, có M là trung điểm của AB suy ra MP vuông góc với AB (2)
Từ (1,2) suy ra M, N, P thẳng hàng
Muốn giải đáp các thắc mắc tới toán , vật lý vui lòng chat trức tiếp

2:
a: A=căn 3-1-2-căn 3=-3
b: =căn 3+căn 2-căn 3+căn 2=2*căn 2
d: =(căn 7/2+căn 5/2)*(căn 7-căn 5)=2/2=1
e: =3-căn 5+2căn 5+2-căn 5+2
=7








Câu 2:
\(3x^2-3x-1=0(*)\)
Theo định lí Vi-ét ta có
\(\begin{cases} S=x_1+x_2=\frac{3}{3}=1\\ P=x_1.x_2=\frac{-1}{3} \end{cases} \)
Theo định lí Vi-ét đảo ta lại có:
Hai nghiệm \(x_1;x_2\) là nghiệm của phương trình: \(X^2-SX+P=0(1)\)
\(\Leftrightarrow X^2-X-\frac{1}{3}=0\)
Ta có: \(\Delta=1+\frac{1}{3}=\frac{4}{3} > 0\)
Vậy phương trình (1) có hai nghiệm phân biệt:
\(\begin{cases} X_1=\frac{3+\sqrt{\frac{4}{3}}}{6}\\ X_2=\frac{3-\sqrt{\frac{4}{3}}}{6} \end{cases} \)
\(\Leftrightarrow \begin{cases} X_1=\frac{3+\sqrt{21}}{6}\\ X_2=\frac{3-\sqrt{21}}{6} \end{cases} \)
Do đó phương trình (*) có hai nghiệm:
\(\left[\begin{array}{} \begin{cases} X_1=\frac{3+\sqrt{21}}{6}\\ X_2=\frac{3-\sqrt{21}}{6} \end{cases}\\ \begin{cases} X_1=\frac{3-\sqrt{21}}{6}\\ X_2=\frac{3+\sqrt{21}}{6} \end{cases} \end{array} \right.\)
\(\Rightarrow \left | x_1-x_2 \right |=\left | x_2-x_1 \right |\)
\(\Rightarrow \left | x_1-x_2 \right |=\left | \frac{3-\sqrt{21}-3-\sqrt{21}}{6} \right |=\left | \frac{-\sqrt{21}}{3} \right |=\frac{\sqrt{21}}{3}\)
Câu 3: \(\begin{cases} x+3y=7\sqrt{2}\\ -2x+y=0 \end{cases} \)
\(\Leftrightarrow \begin{cases} 7x=7\sqrt{2}(1)\\ y=2x \end{cases} \)
Xét phương trình (1) ta có:
\(x=\sqrt{2}\)
\(\Rightarrow y=2\sqrt{2}\)
Vậy hệ phương trình có nghiệm\((x,y)=(\sqrt{2},2\sqrt{2})\)
Câu 4:
Gọi chiều rộng của thửa ruộng là y(m)
Gọi chiều dài của thửa ruộng là x(m)
Điều kiện: x,y>0
Vì diện tích của thửa ruộng hình chữ nhật là \(10000m^2\) nên ta có phương trình:
\(x.y=10000(1) \)
Vì khi tăng chiều rộng của thửa ruộng thêm 20 m và giảm chiều dài đi 50 m thì diện tích thửa ruộng tăng thêm \(500m^2\) nên ta phương trình:
\((y+20).(x-50)=10000+500(2)\)
Từ phương trình (1) và (2) ta có hệ phương trình:
\(\begin{cases} x.y=10000\\ (y+20).(x-50)=10500 \end{cases} \)
Muộn rồi nên bạn tự giải phương trình này được nha:(
Giải phương trình trên ta nhận được nghiệm(x,y)=(200,50)
Do đó chiều rộng của thửa ruộng là 50m
chiều dài của thửa ruộng là 200m