cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (0). M là điểm thuộc cung nhỏ AC. vẽ MH vuông góc với BC, vẽ MI vuông AC tại I, chứng minh:1. IHM=ICM2.đường thẳng HI cắt đường thẳng AB tại K,. chứng minh: MK vuông BK3. DF cắt EB tại M, HF cắt EC tại N. chứng minh tam giác MIH đồng dạng với MAB4, gọi E là trung điểm IH và F là trung điểm AB. chứng minh tứ giác KMEF nội tiếp, suy ra ME vuông góc...
Đọc tiếp
cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (0). M là điểm thuộc cung nhỏ AC. vẽ MH vuông góc với BC, vẽ MI vuông AC tại I, chứng minh:
1. IHM=ICM
2.đường thẳng HI cắt đường thẳng AB tại K,. chứng minh: MK vuông BK
3. DF cắt EB tại M, HF cắt EC tại N. chứng minh tam giác MIH đồng dạng với MAB
4, gọi E là trung điểm IH và F là trung điểm AB. chứng minh tứ giác KMEF nội tiếp, suy ra ME vuông góc với EF
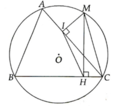
1/Xét tứ giác MIHC có:
góc MIC=90 độ (MI vuông góc với AC tại I)(1)
góc MHC=90 độ (MH vuông góc với BC tại H)(2)
Từ (1) và (2)=> tứ giác MIHC nội tiếp
(tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới một góc 90 độ)
=> góc IHM=góc ICM (cùng chắn cung IM)(đpcm)
2/Tứ giác ABCM nội tiếp (O)
=> góc MCB= góc MAK (3)
Tứ giác MIHC nội tiếp (c/m trên)
=>góc MCB= góc MIK (4)
Từ (3) và (4)=> góc MAK= góc MIK
=> Tứ giác AIMK nội tiếp
(tứ giác có 2 đỉnh kề nhau cùng nhìn cạnh chứa 2 đỉnh còn lại dưới 1 góc an-pha)
=>góc AKM+góc AIM=180 độ
=>góc AKM=90 độ (vì góc AIM= 90 độ)
=>MK vuông góc với BK tại K( đpcm)
Còn câu 3 và 4 đề ko có D và F nên mk ko c/m dc
chị ơi! cái này em chưa học nên chưa biết trả lời lời làm sao mong chị thông cảm