giải phương trình :
3a4 + 3a3 + 13a2 + 16 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VX
7 tháng 4 2021
............................................................................................................................................................................................................................................................................................................................ bạn làm nghề mẹ bạn làm gì ở đâu lớp 3 ko lớp 4 hhhhhhh
CM
26 tháng 12 2017
a) Lớp 3A1 có 35 học sinh ; lớp 3A2 có 34 học sinh.
b) Lớp 3A4 có nhiều hơn lớp 3A5 2 học sinh.
c) Tổng số học sinh của 5 lớp khối 3 là 171 học sinh.
PT
1
CM
1 tháng 9 2019
Đặt m = x 2 .Điều kiện m ≥ 0
Ta có: 1/3. x 4 - 1/2. x 2 +1/6 =0⇔ 2 x 4 -3 x 2 +1=0 ⇔ 2 m 2 -3m + 1 =0
Phương trình 2 m 2 -3m + 1 =0 có hệ số a=2,b=-3,c=1 nên có dạng a +b+c =0
suy ra: m 1 = 1 , m 2 = 1/2
Ta có: x 2 = 1 ⇒ x = ± 1
x 2 = 1/2 ⇒ x = ± 2 /2
Vậy phương trình đã cho có 4 nghiệm :
x 1 =1 ; x 2 =-1 ; x 3 =( 2 )/2; x 4 = - 2 /2
.
.
CM
3 tháng 1 2019
Phương trình bậc hai y2 – 8y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b2 – 4ac = (-8)2 – 4.1.16 = 0.
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
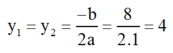
Vậy phương trình có nghiệm kép y = 4.
C
5 tháng 5 2023
`(2x-6)(4x+16)=0`
`@TH1:`
`2x-6=0`
`<=>2x=6`
`<=>x=3`
`@TH2:`
`4x+16=0`
`<=>4x=-16`
`<=>x=-4`
R
5 tháng 5 2023
\(\left(2x-6\right).\left(4x+16\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-6=0\\4x+16=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}2x=6\\4x=-16\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-4\end{matrix}\right.\)
\(S=\left\{3;-4\right\}\)
5 tháng 3 2018
3x ^ 2 -2x-16 = 0
Đơn giản hóa 3x 2 + -2x + -16 = 0 Sắp xếp lại các điều khoản: -16 + -2x + 3x 2 = 0 Giải quyết -16 + -2x + 3x 2 = 0 Giải quyết cho biến 'x'. Yếu tố một trinomial. (-2 + -1x) (8 + -3x) = 0
Bài toán con 1
Đặt các yếu tố '(-2 + -1x)' bằng không và cố gắng để giải quyết: Đơn giản hóa -2 + -1x = 0 Giải quyết -2 + -1x = 0 Di chuyển tất cả các cụm từ có chứa x sang trái, tất cả các thuật ngữ khác ở bên phải. Thêm '2' vào mỗi bên của phương trình. -2 + 2 + -1x = 0 + 2 Kết hợp như các thuật ngữ: -2 + 2 = 0 0 + -1x = 0 + 2 -1x = 0 + 2 Kết hợp như các thuật ngữ: 0 + 2 = 2 -1x = 2 Chia mỗi bên bằng '-1'. x = -2 Đơn giản hóa x = -2
Bài toán con 2
Đặt các yếu tố '(8 + -3x)' bằng không và cố gắng để giải quyết: Đơn giản hóa 8 + -3x = 0 Giải quyết 8 + -3x = 0 Di chuyển tất cả các cụm từ có chứa x sang trái, tất cả các thuật ngữ khác ở bên phải. Thêm '-8' vào mỗi bên của phương trình. 8 + -8 + -3x = 0 + -8 Kết hợp như các thuật ngữ: 8 + -8 = 0 0 + -3x = 0 + -8 -3x = 0 + -8 Kết hợp như các thuật ngữ: 0 + -8 = -8 -3x = -8 Chia mỗi bên bằng '-3'. x = 2.666666667 Đơn giản hóa x = 2.666666667
Dung dịch
x = {-2, 2.666666667}
NHỚ CHO MÌNH THẬT NHIỀU NHA !!!!!!!!!!!!!!!!!!!!
NẾU THẤY ĐÚNG VÀ HAY
5 tháng 3 2018
3x2 -2x-16=0
<=> 3x2+6x-8x-16=0
<=>3x[x+2]-8[x+2]=0
<=> [x+2][3x-8]=0
<=> \(\orbr{\begin{cases}x+2=0\\3x-8=0\end{cases}}\)<=> \(\orbr{\begin{cases}x=-2\\3x=8\end{cases}}\) <=> \(\orbr{\begin{cases}x=-2\\x=\frac{8}{3}\end{cases}}\)
Vậy...
28 tháng 6 2023
2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1
31 tháng 10 2021
ĐKXĐ: \(\left[{}\begin{matrix}x\ge4\\x=-4\end{matrix}\right.\)
\(\Leftrightarrow\sqrt{\left(x-4\right)\left(x+4\right)}=3\sqrt{\left(x+4\right)}\\ \Leftrightarrow\left(x-4\right)\left(x+4\right)=9\left(x+4\right)\\ \Leftrightarrow\left(x+4\right)\left(x-13\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-4\left(tm\right)\\x=13\left(tm\right)\end{matrix}\right.\)
31 tháng 10 2021
ĐKXĐ: \(\left[{}\begin{matrix}x\ge4\\x=-4\end{matrix}\right.\)
\(pt\Leftrightarrow\sqrt{\left(x-4\right)\left(x+4\right)}-3\sqrt{x+4}=0\)
\(\Leftrightarrow\sqrt{x+4}.\left(\sqrt{x-4}-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x+4}=0\\\sqrt{x-4}=3\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x+4=0\\x-4=9\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-4\left(tm\right)\\x=13\left(tm\right)\end{matrix}\right.\)