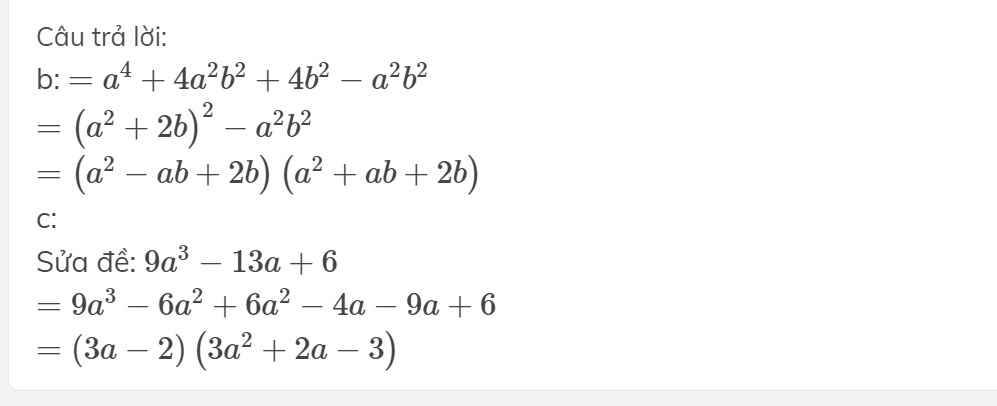KV
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AP
29 tháng 10 2018
a) a4+3a2b2+4b2
=a4+4a2b2+4b2-a2b2
=(a2+2b2)2-a2b2
=(a2+2b2-ab)(a2+2b2+ab)
31 tháng 10 2022
b: =9a^3-4a-9a+6
\(=a\left(3a-2\right)\left(3a+2\right)-3\left(3a-2\right)\)
\(=\left(3a-2\right)\left(3a^2+2a-3\right)\)
24 tháng 10 2022
a: \(=a^4+4a^2b^2+4b^2-a^2b^2\)
\(=\left(a^2+2b\right)^2-a^2b^2\)
\(=\left(a^2+2b-ab\right)\left(a^2+2b+ab\right)\)
b: \(=9a^3-6a^2+6a^2-4a-9a+6\)
\(=\left(3a-2\right)\left(3a^2+2a-3\right)\)
S
18 tháng 10 2018
\(x^4+x^3y-xy^3-y^4=\left(x^4-y^4\right)+\left(x^3y-xy^3\right)\)
\(=\left[\left(x^2\right)^2-\left(y^2\right)^2\right]+xy\left(x^2-y^2\right)\)
\(=\left(x^2+y^2\right)\left(x^2-y^2\right)+xy\left(x+y\right)\left(x-y\right)\)
\(=\left(x^2+y^2\right)\left(x+y\right)\left(x-y\right)+xy\left(x+y\right)\left(x-y\right)\)
\(=\left(x+y\right)\left(x-y\right)\left(x^2+y^2+xy\right)\)
25 tháng 2 2017
a, Đặt \(2^x=t,t>0\)
Pt trở thành: \(t^2-10t+16=0\Leftrightarrow\left(t-2\right)\left(t-8\right)=0\Leftrightarrow\orbr{\begin{cases}t=2\\t=8\end{cases}\left(tm\right)}\)
Nếu t=2 => x=1
nếu t=8=> x=3
Vậy x=...
b, Đặt: \(2x^2-3x-1=t\)
pt trở thành: \(t^2-3\left(t-4\right)-16=0\Leftrightarrow t^2-3t-4=0\Leftrightarrow\left(t+1\right)\left(t-4\right)=0\Leftrightarrow\orbr{\begin{cases}t=-1\\t=4\end{cases}}\)
* Nếu t=-1 <=> \(2x^2-3x-1=-1\Leftrightarrow x\left(2x-3\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)
* Nếu t=4 <=> \(2x^2-3x-1=4\Leftrightarrow2x^2-3x-5=0\Leftrightarrow\left(x+1\right)\left(2x-5\right)=0\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{5}{2}\end{cases}}\)
Vậy x=...
LV
2
20 tháng 1 2019
a) \(x^3-3x^2+4=0\)
\(\Leftrightarrow\left(x-2\right)^2.\left(x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=2\\x=-1\end{cases}}\)
b) \(\left(2x^2-3x-1\right)^2-3\left(2x^2-3x-5\right)-16=0\)
\(\Leftrightarrow4x^4-12x^3+7x^2+3x=0\)
\(\Leftrightarrow x\left(2x-3\right)\left(2x^2-3x-1\right)=0\)
\(\Leftrightarrow2x-3=0\)
\(\Leftrightarrow2x=0+3\)
\(\Leftrightarrow2x=3\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{3}{2}\end{cases}}\)
KT
5 tháng 2 2018
a) \(x^3-3x^2+4=0\)
\(\Leftrightarrow\)\(x^3+x^2-4x^2-4x+4x+4=0\)
\(\Leftrightarrow\)\(\left(x-1\right)\left(x^2-4x+4\right)=0\)
\(\Leftrightarrow\)\(\left(x-1\right)\left(x-2\right)^2=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x-1=0\\x-2=0\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=1\\x=2\end{cases}}\)
Vậy....
DH
20 tháng 8 2017
a, \(\dfrac{3a^2b-4ab^2}{5ab}=\dfrac{ab\left(3a-4b\right)}{5ab}=\dfrac{3a-4b}{5}\)
b, \(\dfrac{3x^3y^2-5x^2y^3+4x^3y^3}{x^2y^2}=\dfrac{x^2y^2\left(3x-5y+4xy\right)}{x^2y^2}\)
\(=3x-5y+4xy\)
c, \(\dfrac{2a^5b^4+3a^4b^3}{-3a^4b^5}=\dfrac{a^4b^3\left(2ab+3\right)}{-3a^4b^5}=\dfrac{2ab+3}{-3b^2}\)
d, \(\dfrac{-a^5b^4+3a^6b^2}{4a^4b^2}=\dfrac{-a^4b^2\left(ab^2+3a^2\right)}{4a^4b^2}=\dfrac{-\left(ab^2+3a^2\right)}{4}\)
Chúc bạn học tốt!!!
20 tháng 8 2017
a. \(\left(3a^2b-4ab^3\right):5ab=3a^2b:5ab-4ab^3:5ab=\dfrac{3}{5}a-\dfrac{4}{5}b^2\)
b. \(\left(3x^3y^2-5x^2y^3+4x^3y^3\right):x^2y^2=3x^3y^2:x^2y^2-5x^2y^3:x^2y^2+4x^3y^3:x^2y^2=3x-5y+4xy\)
c. \(\left(2a^5b^4+3a^4b^3\right):\left(-3a^4b^5\right)=2a^5b^4:\left(-3a^4b^5\right)+3a^4b^3:\left(-3a^4b^5\right)=-\dfrac{2a}{3b}-\dfrac{1}{b^2}\)
d. \(\left(-a^5b^4+3a^6b^2\right):4a^4b^2=\left(-a^5b^4\right):4a^4b^2+3a^6b^2:4a^4b^2=-\dfrac{1ab^2}{4}+\dfrac{3a^2}{4}\)
3 tháng 12 2022
1: =(4x-1)^2-3(4x-1)
=(4x-1)(4x-1-3)
=4(x-1)(4x-1)
2: =-8x^4y^5(2y+3x)
3: =(a-5)^2-4b^2
=(a-5-2b)(a-5+2b)
5: =x^2-mx-nx+mn
=x(x-m)-n(x-m)
=(x-m)(x-n)
6: =(4a^2-3a-18-4a^2-3a)(4a^2-3a-18+4a^2+3a)
=(-6a-18)(8a^2-18)
=-6(2a-3)(2x+3)(a+3)