Cho Tam giác ABC có a cos B = b cos A Chứng minh Tam giác ABC cân tại Cc
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
M
1
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2020
\(\Leftrightarrow sinA=2sinB.cosC\)
\(\Leftrightarrow\dfrac{a}{2R}=2.\dfrac{b}{2R}.\dfrac{a^2+b^2-c^2}{2ab}\)
\(\Leftrightarrow a^2=a^2+b^2-c^2\)
\(\Leftrightarrow b^2=c^2\Leftrightarrow b=c\)
Vậy tam giác ABC cân tại A
PT
1
QT
1
HQ
Hà Quang Minh
Giáo viên
25 tháng 9 2023
Ta có: \(A+B+C=180^o\)
a)
\(\sin (B + C) = \sin \left( {{{180}^o} - A} \right) = \sin A\)
Vậy \(\sin A = \sin \;(B + C)\)
b)
\(\cos (B + C) = \cos \left( {{{180}^o} - A} \right) = - \cos A\)
Vậy \(\cos A = - \cos \;(B + C)\)
HT
25 tháng 12 2015
a) Do A + B + C = 180 độ nên góc A bù với góc B + C => sin(B + C) = sinA (sin hai góc bù bằng nhau)
(A + B)/2 + C/2 = 90 độ => hai góc (A + B)/2 và C/2 là hai góc phụ nhau => cos (A + B)/2 = sin(C/2) (Chắc đề bài bạn cho nhầm thành sinC)
b) Bạn xem lại đề nhé
c) \(sin^6a+cos^6a+3sin^2a.cos^2a=\left(sin^2a\right)^3+\left(cos^2a\right)^3+3.sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)\left(sin^4a+cos^4a-sin^2a.cos^2a\right)+3sin^2a.cos^2a\)
= \(sin^4a+cos^4a+2sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)^2=1\)
PT
1
CM
2 tháng 7 2018
A, B , C là ba góc của ΔABC nên ta có: A + B + C = 180º
a) sin A = sin (180º – A) = sin (B + C)
b) cos A = – cos (180º – A) = –cos (B + C)
GH
1
17 tháng 10 2021
Kẻ đg cao AH thì AH cũng là trung tuyến
Do đó \(BH=\dfrac{1}{2}BC=5\left(cm\right)\)
\(\Rightarrow\cos\widehat{B}=\dfrac{BH}{AB}=\dfrac{5}{13}\)
MN
2
29 tháng 7 2023
\(1+tan^2B=1+\left(\dfrac{AC}{AB}\right)^2=\dfrac{AC^2+AB^2}{AB^2}=\dfrac{BC^2}{AB^2}\)
\(=\dfrac{1}{\left(\dfrac{AB}{BC}\right)^2}\)
\(=\dfrac{1}{cos^2B}\)
28 tháng 7 2023
1+tan^2B
=1+(AC/AB)^2
=AB^2/AB^2+AC^2/AB^2
=BC^2/AB^2
=1:(AB/BC)^2
=1:cos^2B
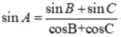
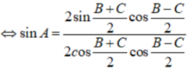
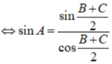
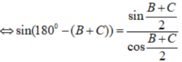
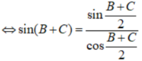
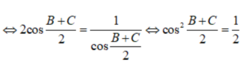
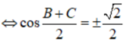
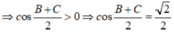
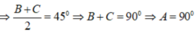
Áp dụng hệ quả định lí hàm Cos ta có:
a.cosB=b.cosA\\ \Leftrightarrow a.\dfrac{a^2+c^2-b^2}{2ac}=b.\dfrac{b^2+c^2-a^2}{2bc}\\a.cosB=b.cosA⇔a.2aca2+c2−b2=b.2bcb2+c2−a2
\Leftrightarrow\dfrac{a^2+c^2-b^2}{2c}=\dfrac{b^2+c^2-a^2}{2c}\\⇔2ca2+c2−b2=2cb2+c2−a2
\Leftrightarrow a^2+c^2-b^2=b^2+c^2-a^2\\⇔a2+c2−b2=b2+c2−a2
\Leftrightarrow a^2-b^2=b^2-a^2\\ \Rightarrow a=b⇔a2−b2=b2−a2⇒a=b
Vậy tam giác ABC cân tại C