Cho hình chóp S.ABC, đáy ABC là tam giác đều cạnh a. H là trung diểm của AB, SH ⊥ (ABC), SH = a\(\sqrt{3}\) , M là trung điểm SA.
Tính khoảng cách từ M đến mặt phẳng (SBC)
Mọi người giúp em với !!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
22 tháng 2 2018
Đáp án B
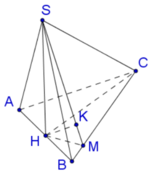
Ta có tam giác HBM đồng dạng với tam giác CBA nên
Xét tam giác vuông SHC có
5 tháng 4 2016
Theo giả thiết, \(HA=HC=\frac{1}{2}AC=a\) và \(SH\perp\left(ABC\right)\)
Xét \(\Delta v.ABC\) ta có : \(BC=AC.\cos\widehat{ACB}=2a\cos30^0=\sqrt{3}a\)
Do đó : \(S_{\Delta.ABC}=\frac{1}{2}AC.BC.\sin\widehat{ACB}=\frac{1}{2}.2a.\sqrt{3}a.\sin30^0=\frac{\sqrt{3}a^2}{2}\)
Vậy \(V_{S.ABC}=\frac{1}{3}SH.S_{ABC}=\frac{1}{3}.\sqrt{2}a.\frac{\sqrt{3}}{2}a^2=\frac{\sqrt{6}a^3}{6}\)
Vì CA=2HA nên d(C,(SAB))=2d(H, (SAB)) (1)
Gọi N là trung điểm của Ab, ta có HN là đường trung bình của tam giác ABC
Do đó HN//BC suy ra AB vuông góc với HN.
Lại có AB vuông góc với Sh nên AB vuông góc với mặt phẳng (SHN).
Do đó mặt phẳng (SAB) vuông góc với mặt phẳng (SHN).
Mà Sn là giao tuyến của 2 mặt phẳng vừa nêu, nên trong mặt phẳng (SHN), hạ HK vuông góc với SN, ta có HK vuông góc với mặt phẳng (SAB)
Vì vậy d(J, (SAB)) = HK. Kết hợp với (1), suy ra d(C. (SAB))=2HK (2)
Vì \(SH\perp\left(ABC\right)\) nên \(SH\perp HN\), xét tam giác v.SHN, ta có :
\(\frac{1}{HK^2}=\frac{1}{SH^2}+\frac{1}{HN^2}=\frac{1}{2a^2}+\frac{1}{HN^2}\)
Vì HN là đường trung bình của tam giác ABC nên \(HN=\frac{1}{2}BC=\frac{\sqrt{3}a}{2}\)
Do \(\frac{1}{HK^2}=\frac{1}{2a^2}+\frac{4}{3a^2}=\frac{11}{6a^2}\) suy ra \(HK=\frac{\sqrt{66}a}{11}\) (3)
Thế (3) vào (2) ta được \(d\left(C,\left(SAB\right)\right)=\frac{\sqrt{66}a}{11}\)
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 3 2021
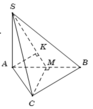
Trong mp (SAB), qua B dựng đường thẳng song song SH, cắt tia AS kéo dài tại D
\(\Rightarrow\) SH là đường trung bình tam giác ABD \(\Rightarrow BD=2SH\) và \(BD\perp\left(ABC\right)\)
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\Rightarrow AC\perp\left(BDM\right)\)
Trong mp (BDM), kẻ \(BK\perp DM\Rightarrow BK\perp\left(SAC\right)\Rightarrow\widehat{BSK}\) là góc giữa SB và (SAC)
\(\Rightarrow\widehat{BSK}=45^0\Rightarrow SB=BK\sqrt{2}\)
\(\Rightarrow AD=2SA=2SB=2\sqrt{2}BK\Rightarrow BD^2=AD^2-AB^2=8BK^2-4a^2\) (1)
Mặt khác: \(\dfrac{1}{BK^2}=\dfrac{1}{BM^2}+\dfrac{1}{BD^2}\Rightarrow\dfrac{1}{BK^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\) (2)
(1);(2) \(\Rightarrow\left\{{}\begin{matrix}BD^2=8BK^2-4a^2\\\dfrac{1}{BK^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\end{matrix}\right.\)
\(\Rightarrow\dfrac{8}{BD^2+4a^2}-\dfrac{1}{BD^2}=\dfrac{1}{3a^2}\Rightarrow BD\Rightarrow SH\)
Sao kết quả xấu vậy nhỉ?
CM
22 tháng 12 2017
Xác định được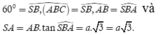 
Do M là trung điểm của cạnh AB nên 
Tam giác vuông SAM, có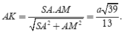 
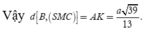
Chọn B.
Do M là trung điểm SA, H là trung điểm AB \(\Rightarrow HM\) là đường trung bình tam giác SAB
\(\Rightarrow HM||SB\Rightarrow HM||\left(SBC\right)\)
\(\Rightarrow d\left(M;\left(SBC\right)\right)=d\left(H;\left(SBC\right)\right)\)
Trong mp (ABC) từ H kẻ \(HD\perp BC\), trong mp (SHD) từ H kẻ \(HE\perp SD\)
\(\Rightarrow HE\perp\left(SBC\right)\Rightarrow HE=d\left(H;\left(SBC\right)\right)\)
\(HD=HB.sinB=\dfrac{a}{2}.sin60^0=\dfrac{a\sqrt{3}}{4}\)
Hệ thức lượng trong tam giác vuông SHD:
\(\dfrac{1}{HE^2}=\dfrac{1}{SH^2}+\dfrac{1}{HD^2}\Rightarrow HE=\dfrac{SH.HD}{\sqrt{SH^2+HD^2}}=\dfrac{a\sqrt{51}}{17}\)
\(\Rightarrow d\left(M;\left(SBC\right)\right)=HE=\dfrac{a\sqrt{51}}{17}\)