Các bn ơi giúp mik câu này nhé!
27,93 = 27 + \(\begin{matrix}93\\100\end{matrix}\) Đúng hay Sai
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Ta có: \(9x^4+8x^2-1=0\)
\(\Leftrightarrow9x^4+9x^2-x^2-1=0\)
\(\Leftrightarrow9x^2\left(x^2+1\right)-\left(x^2+1\right)=0\)
\(\Leftrightarrow\left(x^2+1\right)\left(9x^2-1\right)=0\)
mà \(x^2+1>0\forall x\)
nên \(9x^2-1=0\)
\(\Leftrightarrow9x^2=1\)
\(\Leftrightarrow x^2=\dfrac{1}{9}\)
hay \(x\in\left\{\dfrac{1}{3};-\dfrac{1}{3}\right\}\)
Vậy: \(S=\left\{\dfrac{1}{3};-\dfrac{1}{3}\right\}\)

b)\(\left\{{}\begin{matrix}3x-2y=4\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2\left(5-2x\right)=4\\y=5-2x\end{matrix}\right.\)\(\)\(\Leftrightarrow\)\(\left\{{}\begin{matrix}3x-10+4x=4\\y=5-2x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7x=14\\y=5-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Vậy nghiệm duy nhất của hpt là: (2;1)
c) \(\left\{{}\begin{matrix}2y-x=2\\2x-y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2y-2\\2\left(2y-2\right)-y=-1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2y-2\\4y-4-y=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2y-2\\3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)
Vậy nghiệm duy nhất của hpt là: (0;1)
a) \(\left\{{}\begin{matrix}x+2y=2\left(1\right)\\-2x+y=1\left(2\right)\end{matrix}\right.\)
Từ (1): \(x=2-2y\) (3)
Thế (3) vào (2), ta được: \(-2\left(2-2y\right)+y=1< =>-4+4y+y=1\)
\(\Leftrightarrow y=1\)\(\Rightarrow\)\(x=2-2.1=0\)
Vậy nghiệm duy nhất của hpt là: (0;1)

\(\left\{{}\begin{matrix}x-2y=3\left(1\right)\\x^2+xy-5y=25\left(2\right)\end{matrix}\right.\)
\(\left(2\right)\Leftrightarrow x^2+xy-5y-25=0\)
\(\Delta=b^2-4ac=\left(y+10\right)^2\ge0\)
=> phương trình (2) có 2 nghiệm \(\left\{{}\begin{matrix}x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=5\\x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=-y-5\end{matrix}\right.\)
- với x=5 thì y=1
-với x=-y-5 thay vào (1)=> y=\(-\dfrac{8}{3}\);\(x=-\dfrac{7}{3}\)

ĐKXĐ: \(x\ne y,x\ne-y\)
\(hpt\Leftrightarrow\left(\dfrac{1}{x+y}+\dfrac{1}{x-y}\right)-\left(\dfrac{1}{x+y}+\dfrac{1}{x-y}\right)=\dfrac{5}{8}-\dfrac{3}{8}\)
\(\Leftrightarrow0=\dfrac{1}{4}\left(VLý\right)\)
Vậy hpt vô nghiệm

Lời giải:
Tất cả những bài này đều có hướng giải y chang nhau, nên mình hướng dẫn mẫu 1 bài, các bài khác bạn triển khai tương tự
4. \(\left\{\begin{matrix} 2x-y=5\\ -x+y=-2\end{matrix}\right.\)
Từ PT(1) ta có: $y=2x-5$ (biểu diễn $y$ theo $x$). Thay vào PT(2):
$-x+(2x-5)=-2$
$\Leftrightarrow x-5=-2$
$\Leftrightarrow x=3$
Khi đó: $y=2x-5=2.3-5=1$
Vậy $(x,y)=(3,1)$
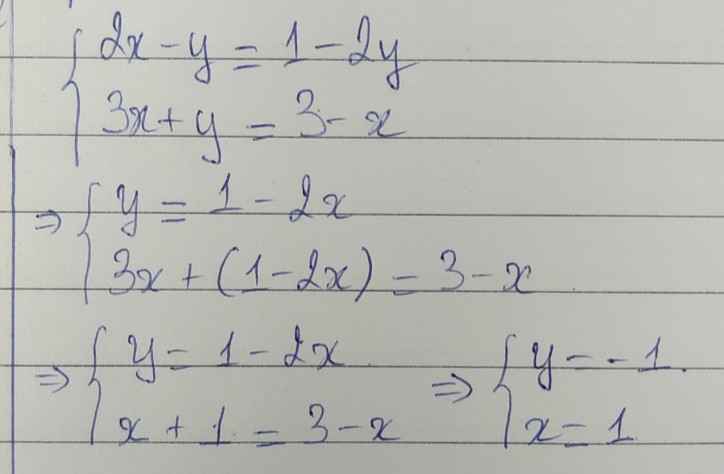
27,93 = 27 + \(\dfrac{93}{100}\)
27,93 = 27 + 0,93
27,93 = 27,93
vậy 27,93 = 27 + \(\dfrac{93}{100}\) là Đúng
Đúng