Cho hình vẽ sau:
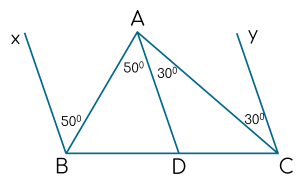
Chứng minh $Bx$ // $Cy$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DX
20 tháng 12 2022
Hình Tự Vẽ nhe
a)
Tam Giác ABC có:
E là trung điểm của AB (gt)
K là trung điểm của AC(gt)
=> EK là đường trung bình của tam giác ABC
=> EK//BC ( tính chất đường trung bình của tam giác )
b)
Tứ giác ABMC có:
BM//AC ( Bx//AC; M thuộc Bx)
CM//AB ( Cy//AB; M thuộc Cy )
Góc A = 90 độ (gt)
=> tứ giác ABMC là Hình chữ nhật
=> AB//MC (tính chất hình chữ nhật )
c)
Ta có: AB // KO ( Từ K vẽ đường thẳng song song với AB cắt BC tại O )
mà AB//MC(cmt) => MC//KO
Tam Giác ABC có:
K là trung điểm của AC (gt)
KO // AB ( Từ K vẽ đường thẳng song song với AB cắt BC tại O )
=> KO là đường trung bình của tam giác ABC
=> O là trung điểm của BC ( tính chất đường trung bình trong tam giác )
tam giác AMC có:
K là trung điểm của AC (gt)
KO//MC (cmt)
=> KO là đường trung bình của tam giác AMC => O là trung điểm của AM ( tính chất đường trung bình trong tam giác )
Vì tứ giác ABMC là Hình chữ nhật => AM Cắt BC tại trung điểm của Mỗi đường mà O là trung điểm của AM và BC => AM cắt BC tại O => A;M;O Thẳng hàng
NT
0
29 tháng 11 2023
a) Để chứng minh tứ giác ABDC là hình chữ nhật, ta cần chứng minh AB || CD và AB = CD.
Vì Bx vuông góc với AB, nên AB || Bx.
Vì Cy vuông góc với AC, nên AC || Cy.
Do đó, AB || CD.
Ta có:
- Góc ABC = 90 độ (vì tam giác ABC vuông tại A).
- Góc BAC = 90 độ (vì Bx vuông góc với AB).
- Góc ACB = 90 độ (vì Cy vuông góc với AC).
Vậy tứ giác ABDC có 4 góc vuông, tức là là hình chữ nhật.
b) Gọi M là điểm đối xứng của B qua A và N là điểm đối xứng của C qua A. Ta cần chứng minh tứ giác BCMN là hình thoi và AD = MC.
Vì M là điểm đối xứng của B qua A, nên AM = MB và góc AMB = góc BMA = 90 độ.
Vì N là điểm đối xứng của C qua A, nên AN = NC và góc ANC = góc CNA = 90 độ.
Do đó, ta có:
- AM = MB = MC (vì M là trung điểm của BC).
- AN = NC = NB (vì N là trung điểm của BC).
- Góc BMC = góc BMA + góc AMC = 90 độ + 90 độ = 180 độ (tổng các góc trong tứ giác là 360 độ).
Vậy tứ giác BCMN là hình thoi và AD = MC.
c) Gọi E là trung điểm của AC và F là trung điểm của MN. Ta cần chứng minh EF || ND.
Vì E là trung điểm của AC, nên AE = EC.
Vì F là trung điểm của MN, nên AF = FN.
Do đó, ta có:
- AE = EC = AF = FN.
- Góc AEF = góc AFE = góc NDF = góc NFD = 90 độ (vì E và F lần lượt là trung điểm của AC và MN).
Vậy EF || ND.
7 tháng 10 2021
a: Xét tứ giác BHCD có
BH//CD
CH//BD
Do đó:BHCD là hình bình hành
b: Ta có: BHCD là hình bình hành
nên Hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
hay H,M,D thẳng hàng
Vì \(\widehat{xBA}=\widehat{BAD}\left(=50^o\right)\) mà \(\widehat{xBA}\text{ và }\widehat{BAD}\) là 2 góc so le trong
=> Bx//AD (1)
Vì \(\widehat{DAC}=\widehat{ACy}\left(=30^o\right)\) mà \(\widehat{DAC}\text{ và }\widehat{ACy}\) là 2 góc so le trong
=> AD // Cy (2)
Từ (1) và (2) => Bx // Cy
Ta có:
`@` \(\widehat{ABx}=\widehat{DAB}=50^o\)
`=>Bx////AD` ( 2 góc so le trong bằng nhau ) (1)
`@`\(\widehat{ACy}=\widehat{DAC}=30^o\)
`=>Cy////AD` ( 2 góc so le trong bằng nhau ) (2)
\(\left(1\right);\left(2\right)\Rightarrow\)`Bx////Cy`