ab + bc + cd = abc
mik đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\text{#3107}\)
1.
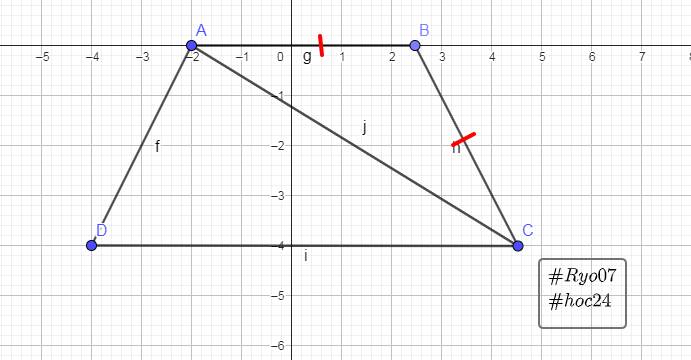
Ta có: \(\text{AB // CD}\)
\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{ACD}}\left(\text{2 góc sole trong}\right)\) `(1)`
Xét `\Delta ABC:`
\(\text{AB = BC (gt)}\)
\(\Rightarrow\) `\Delta ABC` cân tại B
\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{BCA}}\) `(2)`
Từ `(1)` và `(2)`
\(\Rightarrow\widehat{\text{ACB}}=\widehat{\text{ACD}}\)
Mà \(\widehat{\text{ACB}}+\widehat{\text{ACD}}=\widehat{\text{BCD}}\)
\(\Rightarrow\) CA là phân giác của \(\widehat{\text{BCD}}.\)

a.AC = 1/3 AB = 1/3 x 18 = 6 cm
Diện tích ABC là: 1/2 x 6 x 18 = 54 cm vuông

cho ab+bc+ac =1 tính P= (a+b+c-abc)^2/(a^2+1)(b^2+1)(c^2+1)
Ai giúp mik với mik đang cần gấp
help me

Lời giải:
Có:
$(a^2+1)(b^2+1)(c^2+1)=(a^2+ab+bc+ac)(b^2+ab+bc+ac)(c^2+ab+bc+ac)$
$=(a+b)(a+c)(b+c)(b+a)(c+a)(c+b)=[(a+b)(b+c)(c+a)]^2$
Và:
$(a+b+c-abc)^2=[(a+b+c)(ab+bc+ac)-abc]^2$
$=[ab(a+b)+bc(b+c)+ca(c+a)+2abc]^2$
$=[ab(a+b+c)+bc(b+c+a)+ca(c+a)]^2$
$=[(a+b+c)(ab+bc)+ca(c+a)]^2=[b(a+b+c)(a+c)+ac(c+a)]^2$
$=[(c+a)(ab+b^2+bc+ac)]^2=[(c+a)(b+a)(b+c)]^2$
Do đó: $P=\frac{[(a+b)(b+c)(c+a)]^2}{[(a+b)(b+c)(c+a)]^2}=1$

Xét tứ giác ABCD có
AB=BC=CD=AD
nên ABCD là hình thoi
Suy ra: \(\widehat{A}=\widehat{C}\)
mà \(\widehat{A}=\widehat{B}\)
nên \(\widehat{B}=\widehat{C}=90^0\)
\(\Leftrightarrow\widehat{A}=\widehat{D}=90^0\)

Xét △ABC, có \(\widehat{A}=90^0\)
Áp dụng định lý pitago trong tam giác vuông ABC, CÓ
\(BC^2=AB^2+AC^2=2^2+2^2=4+4=8\)
\(\Rightarrow BC=\sqrt{8}=2\sqrt{2}cm\)
Áp dụng định lí pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
hay \(BC^2=2^2+2^2=8\)
⇔\(BC=\sqrt{8}=2\sqrt{2}cm\)
Vậy: \(BC=2\sqrt{2}cm\)
thiếu dữ kiện